Кроме выборочной средней и выборочной дисперсии применяются и другие характеристики вариационного ряда.
Модой 
называют варианту, которая имеет наибольшую частоту.
Например, для ряда
.
Медианой 
называют варианту, которая делит вариационный ряд на две части, равные по числу вариант.
Например, для ряда
.
Для ряда, где чётное число вариант медиана рассчитывается как среднее арифметическое из двух средних вариант.
Например, для ряда
.
Размахом варьирования R называют разность между наибольшей и наименьшей вариантами: 
.
Например, для ряда
.
Средним абсолютным отклонением 
называют среднее арифметическое абсолютных отклонений: 
.
Например, для ряда
.
.
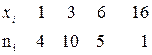
Среднее абсолютное отклонение служит для характеристики рассеяния вариационного ряда.
Коэффициентом вариации V называют выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней: 
.
Ход работы
1. Ознакомиться с теоретической частью данной работы (лекции, учебник).
2. Выполнить задание по своему варианту.
3. Составить отчет по работе.
4. Защитить работу.
Содержание отчета
1. Тема.
2. Цель работы.
3. Ход работы.
4. Решение своего варианта.
10.4 Варианты заданий для самостоятельной работы
Вариант №1
1. По данному распределению выборки найти выборочную среднюю, выборочную дисперсию и построить полигон частот.
2. Найти доверительный интервал для оценки с надёжностью 0,99 неизвестного математического ожидания а нормально распределённого признака Х генеральной совокупности, если известны генеральное среднее квадратическое отклонение 
=4, выборочная средняя 
=10,2 и объём выборки n=16.
3. По данным выборки объёма n из генеральной совокупности нормально распределённого количественного признака найдено «исправленное» среднее квадратическое отклонение s. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надёжностью 0,999 если n=10, s=5,1.
4. По данному распределению выборки (см. задание №1) найти характеристики вариационного ряда (моду, медиану, размах варьирования, среднее абсолютное отклонение, коэффициент вариации).
Вариант №2
1. По данному распределению выборки найти выборочную среднюю, выборочную дисперсию и построить полигон частот.
2. Найти доверительный интервал для оценки с надёжностью 0,99 неизвестного математического ожидания а нормально распределённого признака Х генеральной совокупности, если известны генеральное среднее квадратическое отклонение =5, выборочная средняя =16,8 и объём выборки n=25.
3. По данным выборки объёма n из генеральной совокупности нормально распределённого количественного признака найдено «исправленное» среднее квадратическое отклонение s. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надёжностью 0,999 если n=50, s=14.
4. По данному распределению выборки (см. задание №1) найти характеристики вариационного ряда (моду, медиану, размах варьирования, среднее абсолютное отклонение, коэффициент вариации).
Вариант №3
1. По данному распределению выборки найти выборочную среднюю, выборочную дисперсию и построить полигон частот.
2. Найти доверительный интервал для оценки с надёжностью 0,999 неизвестного математического ожидания а нормально распределённого признака Х генеральной совокупности, если известны генеральное среднее квадратическое отклонение =4, выборочная средняя =10,2 и объём выборки n=16.
3. По данным выборки объёма n из генеральной совокупности нормально распределённого количественного признака найдено «исправленное» среднее квадратическое отклонение s. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надёжностью 0,99 если n=10, s=5,1.
4. По данному распределению выборки (см. задание №1) найти характеристики вариационного ряда (моду, медиану, размах варьирования, среднее абсолютное отклонение, коэффициент вариации).
Вариант №4
1. По данному распределению выборки найти выборочную среднюю, выборочную дисперсию и построить полигон частот.
2. Найти доверительный интервал для оценки с надёжностью 0,999 неизвестного математического ожидания а нормально распределённого признака Х генеральной совокупности, если известны генеральное среднее квадратическое отклонение =5, выборочная средняя =16,8 и объём выборки n=25.
3. По данным выборки объёма n из генеральной совокупности нормально распределённого количественного признака найдено «исправленное» среднее квадратическое отклонение s. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надёжностью 0,99 если n=50, s=14.
4. По данному распределению выборки (см. задание №1) найти характеристики вариационного ряда (моду, медиану, размах варьирования, среднее абсолютное отклонение, коэффициент вариации).
Вопросы к защите практической работы №10
1. В чём состоит сущность выборочного метода? Примеры.
2. Что называется выборкой, генеральной совокупностью, объёмом совокупности? Примеры.
3. Какая выборка называется повторной (бесповторной)?
4. Какие существуют способы отбора? Примеры.
5. Что такое статистическое распределение выборки?
6. Дать определение эмпирической функции распределения.
7. Что такое полигон и гистограмма? Правила построения.
8. Виды оценок.
9. Генеральная и выборочная средняя.
10. Понятие точечной и интервальной оценки.
11. Характеристики вариационного ряда.
Список использованных источников
1 Гмурман, В.Е. Теория вероятностей и математическая статистика/ В.Е. Гмурман. – М.:Высшая школа, 2008. – 479 с.
2 Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике/ В.Е. Гмурман. – М.: Высшее образование, 2008. – 404 с.
3 Кочетков, Е.С. Теория вероятностей и математическая статистика/ Е.С. Кочетков – М.:ФОРУМ:ИНФРА-М, 2007. – 240 с.
4 Колемаев, В.А. Теория вероятностей и математическая статистика/ В.А. Колемаев – М.: ИНФРА-М, 2007. – 356 с.
5 Вентцель, Е.С. Задачи и упражнения по теории вероятностей/ Е.С. Вентцель, Л.А. Овчаров– М.: Издательский центр «Академия», 2008. – 448 с.
6 Кремер, Н.Ш. Теория вероятностей и математическая статистика/ Н.Ш. Кремер – М.: ЮНИТИ-ДАНА, 2008. – 573 с.
Приложение А
(обязательное)
Таблица значений функции 
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 | 0,3989 0,3970 0,3910 0,3814 0,3683 0,3521 0,3332 0,3123 0,2897 0,2661 0,2420 0,2179 0,1942 0,1714 0,1497 0,1295 0,1109 0,0940 0,0790 0,0656 0,0540 0,0440 0,0355 0,0283 0,0224 0,0175 0,0136 0,0104 0,0079 0,0060 0,0044 0,0033 0,0024 0,0017 0,0012 0,0009 0,0006 0,0004 0,0003 0,0002 | 0,3989 0,3965 0,3902 0,3802 0,3668 0,3503 0,3312 0,3101 0,2874 0,2637 0,2396 0,2155 0,1919 0,1691 0,1476 0,1276 0,1092 0,0925 0,0775 0,0644 0,0529 0,0431 0,0347 0,0277 0,0219 0,0171 0,0132 0,0101 0,0077 0,0058 0,0043 0,0032 0,0023 0,0017 0,0012 0,0008 0,0006 0,0004 0,0003 0,0002 | 0,3989 0,3961 0,3894 0,3790 0,3652 0,3485 0,3292 0,3079 0,2850 0,2613 0,2371 0,2131 0,1895 0,1669 0,1456 0,1257 0,1074 0,0909 0,0761 0,0632 0,0519 0,0422 0,0339 0,0270 0,0213 0,0167 0,0129 0,0099 0,0075 0,0056 0,0042 0,0031 0,0022 0,0016 0,0012 0,0008 0,0006 0,0004 0,0003 0,0002 | 0,3988 0,3956 0,3885 0,3778 0,3637 0,3467 0,3271 0,3056 0,2827 0,2589 0,2347 0,2107 0,1872 0,1647 0,1435 0,1238 0,1057 0,0893 0,0748 0,0620 0,0508 0,0413 0,0332 0,0264 0,0208 0,0163 0,0126 0,0096 0,0073 0,0055 0,0040 0,0030 0,0022 0,0016 0,0011 0,0008 0,0005 0,0004 0,0003 0,0002 | 0,3986 0,3951 0,3876 0,3765 0,3621 0,3448 0,3251 0,3034 0,2803 0,2565 0,2323 0,2083 0,1849 0,1626 0,1415 0,1219 0,1040 0,0878 0,0734 0,0608 0,0498 0,0404 0,0325 0,0258 0,0203 0,0158 0,0122 0,0093 0,0071 0,0053 0,0039 0,0029 0,0021 0,0015 0,0011 0,0008 0,0005 0,0004 0,0003 0,0002 | 0,3984 0,3945 0,3867 0,3752 0,3605 0,3429 0,3230 0,3011 0,2780 0,2541 0,2299 0,2059 0,1826 0,1604 0,1394 0,1200 0,1023 0,0863 0,0721 0,0596 0,0488 0,0396 0,0317 0,0252 0,0198 0,0154 0,0119 0,0091 0,0069 0,0051 0,0038 0,0028 0,0020 0,0015 0,0010 0,0007 0,0005 0,0004 0,0002 0,0002 | 0,3982 0,3939 0,3857 0,3739 0,3589 0,3410 0,3209 0,2989 0,2756 0,2516 0,2275 0,2036 0,1804 0,1582 0,1374 0,1182 0,1006 0,0848 0,0707 0,0584 0,0478 0,0387 0,0310 0,0246 0,0194 0,0151 0,0116 0,0088 0,0067 0,0050 0,0037 0,0027 0,0020 0,0014 0,0010 0,0007 0,0005 0,0003 0,0002 0,0002 | 0,3980 0,3932 0,3847 0,3726 0,3572 0,3391 0,3187 0,2966 0,2732 0,2492 0,2251 0,2012 0,1781 0,1561 0,1354 0,1163 0,0989 0,0833 0,0694 0,0573 0,0468 0,0379 0,0303 0,0241 0,0189 0,0147 0,0113 0,0086 0,0065 0,0048 0,0036 0,0026 0,0019 0,0014 0,0010 0,0007 0,0005 0,0003 0,0002 0,0002 | 0,3977 0,3925 0,3836 0,3712 0,3555 0,3372 0,3166 0,2943 0,2709 0,2468 0,2227 0,1989 0,1757 0,1539 0,1334 0,1145 0,0973 0,0818 0,0681 0,0562 0,0459 0,0371 0,0297 0,0235 0,0184 0,0143 0,0110 0,0084 0,0063 0,0047 0,0035 0,0025 0,0018 0,0013 0,0009 0,0007 0,0005 0,0003 0,0002 0,0001 | 0,3973 0,3918 0,3825 0,3697 0,3538 0,3352 0,3144 0,2920 0,2685 0,2444 0,2203 0,1965 0,1736 0,1518 0,1315 0,1127 0,0957 0,0804 0,0669 0,0551 0,0449 0,0363 0,0290 0,0229 0,0180 0,0139 0,0107 0,0081 0,0061 0,0046 0,0034 0,0025 0,0018 0,0013 0,0009 0,0006 0,0004 0,0003 0,0002 0,0001 |
Приложение Б
(обязательное)
Таблица значений функции 
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,20 0,21 0,22 0,23 0,24 0,25 0,26 0,27 0,28 0,29 0,30 0,31 0,32 0,33 0,34 0,35 0,36 0,37 0,38 0,39 0,40 0,41 0,42 0,43 0,44 0,45 0,46 | 0,0000 0,0040 0,0080 0,0120 0,0160 0,0199 0,0239 0,0279 0,0319 0,0359 0,0398 0,0438 0,0478 0,0517 0,0557 0,0596 0,0636 0,0675 0,0714 0,0753 0,0793 0,0832 0,0871 0,0910 0,0948 0,0987 0,1026 0,1064 0,1103 0,1141 0,1179 0,1217 0,1255 0,1293 0,1331 0,1368 0,1406 0,1443 0,1480 0,1517 0,1554 0,1591 0,1628 0,1664 0,1700 0,1736 0,1772 | 0,47 0,48 0,49 0,50 0,51 0,52 0,53 0,54 0,55 0,56 0,57 0,58 0,59 0,60 0,61 0,62 0,63 0,64 0,65 0,66 0,67 0,68 0,69 0,70 0,71 0,72 0,73 0,74 0,75 0,76 0,77 0,78 0,79 0,80 0,81 0,82 0,83 0,84 0,85 0,86 0,87 0,88 0,89 0,90 0,91 0,92 0,93 | 0,1808 0,1844 0,1879 0,1915 0,1950 0,1985 0,2019 0,2054 0,2088 0,2123 0,2157 0,2190 0,2224 0,2257 0,2291 0,2324 0,2357 0,2389 0,2422 0,2454 0,2486 0,2517 0,2549 0,2580 0,2611 0,2642 0,2673 0,2703 0,2734 0,2764 0,2794 0,2823 0,2852 0,2881 0,2910 0,2939 0,2967 0,2995 0,3023 0,3051 0,3078 0,3106 0,3133 0,3159 0,3186 0,3212 0,3238 | 0,94 0,95 0,96 0,97 0,98 0,99 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,18 1,19 1,20 1,21 1,22 1,23 1,24 1,25 1,26 1,27 1,28 1,29 1,30 1,31 1,32 1,33 1,34 1,35 1,36 1,37 1,38 1,39 1,40 | 0,3264 0,3289 0,3315 0,3340 0,3365 0,3389 0,3413 0,3438 0,3461 0,3485 0,3508 0,3531 0,3554 0,3577 0,3599 0,3621 0,3643 0,3665 0,3686 0,3708 0,3729 0,3749 0,3770 0,3790 0,3810 0,3830 0,3849 0,3869 0,3883 0,3907 0,3925 0,3944 0,3962 0,3980 0,3997 0,4015 0,4032 0,4049 0,4066 0,4082 0,4099 0,4115 0,4131 0,4147 0,4162 0,4177 0,4192 | 1,41 1,42 1,43 1,44 1,45 1,46 1,47 1,48 1,49 1,50 1,51 1,52 1,53 1,54 1,55 1,56 1,57 1,58 1,59 1,60 1,61 1,62 1,63 1,64 1,65 1,66 1,67 1,68 1,69 1,70 1,71 1,72 1,73 1,74 1,75 1,76 1,77 1,78 1,79 1,80 1,81 1,82 1,83 1,84 1,85 1,86 1,87 | 0,4207 0,4222 0,4236 0,4251 0,4265 0,4279 0,4292 0,4306 0,4319 0,4332 0,4345 0,4357 0,4370 0,4382 0,4394 0,4406 0,4418 0,4429 0,4441 0,4452 0,4463 0,4474 0,4484 0,4495 0,4505 0,4515 0,4525 0,4535 0,4545 0,4554 0,4564 0,4573 0,4582 0,4591 0,4599 0,4608 0,4616 0,4625 0,4633 0,4641 0,4649 0,4656 0,4664 0,4671 0,4678 0,4686 0,4693 | 1,88 1,89 1,90 1,91 1,92 1,93 1,94 1,95 1,96 1,97 1,98 1,99 2,00 2,02 2,04 2,06 2,08 2,10 2,12 2,14 2,16 2,18 2,20 2,22 2,24 2,26 2,28 2,30 2,32 2,34 2,36 2,38 2,40 2,42 2,44 2,46 2,48 2,50 2,52 2,54 2,56 2,58 2,60 2,62 2,64 2,66 2,68 | 0,4699 0,4706 0,4713 0,4719 0,4726 0,4732 0,4738 0,4744 0,4750 0,4756 0,4761 0,4767 0,4772 0,4783 0,4793 0,4803 0,4812 0,4821 0,4830 0,4838 0,4846 0,4854 0,4861 0,4868 0,4875 0,4881 0,4887 0,4893 0,4898 0,4904 0,4909 0,4913 0,4918 0,4922 0,4927 0,4931 0,4934 0,4938 0,4941 0,4945 0,4948 0,4951 0,4953 0,4956 0,4959 0,4961 0,4963 | 2,70 2,72 2,74 2,76 2,78 2,80 2,82 2,84 2,86 2,88 2,90 2,92 2,94 2,96 2,98 3,00 3,20 3,40 3,60 3,80 4,00 4,50 5,00 | 0,4965 0,4967 0,4969 0,4971 0,4973 0,4974 0,4976 0,4977 0,4979 0,4980 0,4981 0,4982 0,4984 0,4985 0,4986 0,49865 0,49931 0,49966 0,499841 0,499928 0,499968 0,499997 0,499997 |
Приложение В
(обязательное)
Таблица значений 
| n | γ | ||
| 0,95 | 0,99 | 0,999 | |
| ∞ | 2,78 2,57 2,45 2,37 2,31 2,26 2,23 2,20 2,18 2,16 2,15 2,13 2,12 2,11 2,10 2,093 2,064 2,045 2,032 2,023 2,016 2,009 2,001 1,996 1,991 1,987 1,984 1,980 1,960 | 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,06 3,01 2,98 2,95 2,92 2,90 2,88 2,861 2,797 2,756 2,720 2,708 2,692 2,679 2,662 2,649 2,640 2,633 2,627 2,617 2,576 | 8,61 6,86 5,96 5,41 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,02 3,97 3,92 3,883 3,745 3,659 3,600 3,558 3,527 3,502 3,464 3,439 3,418 3,403 3,392 3,374 3,291 |
Приложение Г
(обязательное)
Таблица значений 
| n | γ | ||
| 0,95 | 0,99 | 0,999 | |
| 1,37 1,09 0,92 0,80 0,71 0,65 0,59 0,55 0,52 0,48 0,46 0,44 0,42 0,40 0,39 0,37 0,32 0,28 0,26 0,24 0,22 0,21 0,188 0,174 0,161 0,151 0,143 0,115 0,099 0,089 | 2,67 2,01 1,62 1,38 1,20 1,08 0,98 0,90 0,83 0,78 0,73 0,70 0,66 0,63 0,60 0,58 0,49 0,43 0,38 0,35 0,32 0,30 0,269 0,245 0,226 0,211 0,198 0,160 0,136 0,120 | 5,64 3,88 2,98 2,42 2,06 1,80 1,60 1,45 1,33 1,23 1,15 1,07 1,01 0,96 0,92 0,88 0,73 0,63 0,56 0,50 0,46 0,43 0,38 0,34 0,31 0,29 0,27 0,211 0,185 0,162 |
