Нормальный закон распределения.
Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности
(47)
Нормальный закон распределения также называется законом Гаусса.
Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.
Можно легко показать, что параметры 
и 
, входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х.
Найдем функцию распределения F(x).
(48)
График плотности нормального распределения называется нормальной кривой или кривой Гаусса.
Нормальная кривая обладает следующими свойствами:
1. Функция определена на всей числовой оси.
2. При всех х функция распределения принимает только положительные значения.
3. Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.
4. Найдем экстремум функции.
Т.к. при y’>0 при x<m и y’< 0 при x>m, то в точке х=т функция имеет максимум, равный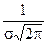 
.
5. Функция является симметричной относительно прямой х=а, т.к. разность (х – а) входит в функцию плотности распределения в квадрате.
6. Для нахождения точек перегиба графика найдем вторую производную функции плотности.
При x=m +s и x=m -s вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.
В этих точках значение функции равно 
.
Построим график функции плотности распределения (см. рис. 10).
Рис. 10
Построены графики при т =0 и трех возможных значениях среднего квадратичного отклонения s=1, s=2 и s=7. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается.
Если а >0, то график сместится в положительном направлении, если а <0 – в отрицательном.
При а =0 и s=1 кривая называется нормированной. Уравнение нормированной кривой:
(49)
Функция Лапласа
Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.
(49)
Обозначим 
Тогда 
(50)
Т.к. интеграл 
не выражается через элементарные функции, то вводится в рассмотрение функция 
, которая называется функцией Лапласа или интегралом вероятностей.
Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах.
Ниже показан график функции Лапласа (см. рис. 8).
Рис. 11
Функция Лапласа обладает следующими свойствами:
1. Ф(0)=0;
2. Ф(- х)=-Ф(х);
3. Ф(¥)=1.
Функцию Лапласа также называют функцией ошибок.
Еще используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:
(51)
Ниже показан график нормированной функции Лапласа (см. рис. 9).
Рис. 12
При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.
Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:
(52)
Если принять D=3s, то получаем с использованием таблиц значений функции Лапласа: 
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.
Это правило называется правилом трех сигм.
На практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.
Пример1. Математическое ожидание и СКО нормально распределено случайной величины равны соответственно 10 и 2. Найти вероятность того, что в результате испытания случайная величина Х примет значение, заключённое в интервале (12; 14).
Решение: Воспользуемся формулой:
P(α< X <β) = Ф(
) – Ф (
)
P( 12<X<14 ) = Ф(
) – Ф (
) = Ф (2)–Ф(1) = 0,4772 – 0,3413 = 0,1359
Пример2. Производится измерение диаметра вала без систематических ошибок. Случайные ошибки измерения Х подчинены нормальному закону распределения со средним квадратическим отклонением σ = 10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.
Решение: Математическое ожидание равно 0, следовательно воспользуемся формулой: P(|X|<δ) = 2Ф(δ/σ)
σ = 10, δ = 15,тогда применяя правило трёх сигм, получим:
P(|X|<15) = 2Ф(15/10) = 2Ф(1,5) = 2∙0,4332 = 0,8664
