Показательное распределение широко используется в теории надежности.
Допустим, некоторое устройство начинает работать в момент времени t0=0, а через какое – то время t происходит отказ устройства.
Обозначим Т непрерывную случайную величину – длительность безотказной работы устройства.
Таким образом, функция распределения F(t)=P(T<t) определяет вероятность отказа за время длительностью t.
Вероятность противоположного события (безотказная работа в течение времени t) равна R(t)= P(T>t)= 1–F(t).
Функцией надежности R(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.
Часто на практике длительность безотказной работы подчиняется показательному закону распределению.
Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.
Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.
Функция надежности для какого - либо устройства при показательном законе распределения равна: 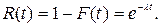
Данное соотношение называют показательным законом надежности.
Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.
Таким образом, безотказная работа устройства зависит только от интенсивности отказов l и не зависит от безотказной работы устройства в прошлом.
Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.
Пример: Длительность безотказной работы прибора имеет показательный закон распределения: F(t) = 1 – e –0,01t (t>0). Найти вероятность того, что за время t=50 часов: а) элемент откажет; б) элемент не откажет.
Решение: Т.к. функция распределения определяет вероятность отказа прибора за время t, то подставив в функцию t=50, получим вероятность отказа:
F (50) = 1 – e –0,01∙50 = 1 – e –0,5 = 1 – 0,606 = 0,394
События «прибор откажет» и «прибор не откажет» являются противоположными, поэтому вероятность того, что прибор не откажет:
Р = 1 – 0,394 = 0,606
Такой же результат можно было получить, используя функцию надёжности:
R (t) = e –λt
R (50) = e –0,01∙50 = 0,606
Ход работы
1. Ознакомиться с теоретической частью данной работы (лекции, учебник).
2. Выполнить задание по своему варианту.
3. Составить отчет по работе.
4. Защитить работу.
Содержание отчета
1. Тема.
2. Цель работы.
3. Ход работы.
4. Решение своего варианта.
9.4 Варианты заданий для самостоятельной работы
Вариант №1
1. Математическое ожидание нормально распределённой случайно величины Х равно a = 3, среднее квадратическое отклонение σ = 2. Написать плотность вероятности.
2. Математическое ожидание и среднее квадратическое отклонение нормально распределённой случайной величины Х соответственно равны 20 и 5. Найти вероятность того, что в результате испытания Х примет значение заключённое в интервале (15,25).
3. Деталь считается годной, если отклонение ее контролируемого размера от проектного не превосходит 10 мм. Случайные отклонения контролируемого размера от проектного починены нормальному закону со средним квадратическим отклонением s=5мм и математическим ожиданием а=0. Сколько процентов годных деталей изготавливает автомат?
4. Случайная величина Х распределена нормально с математическим ожиданием а = 10 и средним квадратическим отклонением σ = 5. Найти интервал, симметричный относительно математического ожидания, в который с вероятностью 0,9973 попадёт величина Х в результате испытания.
5. Непрерывная случайная величина Х распределена по показательному закону, заданному при  плотностью распределения
плотностью распределения  ; при
; при  функции
функции  . Найти вероятность того, что в результате испытания случайная величина Х примет значение из интервала (1,2). Вычислить характеристики НСВ.
. Найти вероятность того, что в результате испытания случайная величина Х примет значение из интервала (1,2). Вычислить характеристики НСВ.
6. Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого  , для второго
, для второго  , для третьего
, для третьего  . Найти вероятность того, что за 5 часов откажут: а) только один элемент; б) не менее двух элементов.
. Найти вероятность того, что за 5 часов откажут: а) только один элемент; б) не менее двух элементов.
Вариант №2
1. Написать плотность вероятности нормально распределённой случайной величины Х, зная, что М (Х) = 3 и D (X) = 16.
2. Математическое ожидание и среднее квадратическое отклонение нормально распределённой случайной величины Х соответственно равны 17 и 8. Найти вероятность того, что в результате испытания Х примет значение заключённое в интервале (5,19).
3. Автомат изготавливает шарики. Шарик считается годным, если отклонение Х диаметра от проектного размера по абсолютной величине меньше 0,7мм. Считая, что случайная величина X распределена нормально со средним квадратическим отклонением s=0,4мм и математическим ожиданием а=0, найти сколько в среднем будет годных шариков среди ста изготовленных?
4. Случайная величина Х распределена нормально со средним квадратическим отклонением σ = 5 мм. Найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 0, 9973 попадёт Х в результате испытания.
5. Непрерывная случайная величина Х распределена по показательному закону, заданному при  плотностью распределения
плотностью распределения  ; при
; при  функции
функции  . Найти вероятность того, что в результате испытания случайная величина Х примет значение из интервала (2,5). Вычислить характеристики НСВ.
. Найти вероятность того, что в результате испытания случайная величина Х примет значение из интервала (2,5). Вычислить характеристики НСВ.
6. Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого  , для второго
, для второго  , для третьего
, для третьего  . Найти вероятность того, что за 10 часов откажут: а) только два элемента; б) не более двух элементов.
. Найти вероятность того, что за 10 часов откажут: а) только два элемента; б) не более двух элементов.
Вариант №3
1. Нормально распределённая случайная величина Х задана плотностью распределения f(X) =  . Найти математическое ожидание и дисперсию Х.
. Найти математическое ожидание и дисперсию Х.
2. Математическое ожидание и среднее квадратическое отклонение нормально распределённой случайной величины Х соответственно равны 20 и 4. Найти вероятность того, что в результате испытания Х примет значение заключённое в интервале (10,20).
3. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону распределения со средним квадратическим отклонением σ = 20 г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10 г.
4. Станок-автомат изготавливает валики, причём контролируется их диаметр Х. Считается, что Х – нормально распределённая случайная величина с математическим ожиданием а = 10 мм и средним квадратическим отклонением σ=0,1мм. Найти интервал, симметричный относительно математического ожидания, в который с вероятностью 0,9973 будут заключены диаметры изготовленных шариков.
5. Непрерывная случайная величина Х распределена по показательному закону, заданному при  плотностью распределения
плотностью распределения  ; при
; при  функции
функции  . Найти вероятность того, что в результате испытания случайная величина Х примет значение из интервала (1,2). Вычислить характеристики НСВ.
. Найти вероятность того, что в результате испытания случайная величина Х примет значение из интервала (1,2). Вычислить характеристики НСВ.
6. Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого  , для второго
, для второго  , для третьего
, для третьего 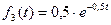 . Найти вероятность того, что за 5 часов откажут: а) только один элемент; б) не менее двух элементов.
. Найти вероятность того, что за 5 часов откажут: а) только один элемент; б) не менее двух элементов.
Вариант №4
1. Дана функция распределения нормального закона
F(X)=  . Найти плотность распределения f (X).
. Найти плотность распределения f (X).
2. Математическое ожидание и среднее квадратическое отклонение нормально распределённой случайной величины Х соответственно равны 15 и 7. Найти вероятность того, что в результате испытания Х примет значение заключённое в интервале (5,12).
3. Автомат изготавливает шарики. Шарик считается годным, если отклонение Х диаметра от проектного размера по абсолютной величине меньше 0,5мм. Считая, что случайная величина X распределена нормально со средним квадратическим отклонением s=0,4мм и математическим ожиданием а=0, найти сколько в среднем будет годных шариков среди ста изготовленных?
4. Случайная величина Х распределена нормально со средним квадратическим отклонением σ = 7 мм. Найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 0, 9973 попадёт Х в результате испытания.
5. Непрерывная случайная величина Х распределена по показательному закону, заданному при  плотностью распределения
плотностью распределения  ; при
; при  функции
функции  . Найти вероятность того, что в результате испытания случайная величина Х примет значение из интервала (3,5). Вычислить характеристики НСВ.
. Найти вероятность того, что в результате испытания случайная величина Х примет значение из интервала (3,5). Вычислить характеристики НСВ.
6. Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого  , для второго
, для второго  , для третьего
, для третьего  . Найти вероятность того, что за 10 часов откажут: а) только два элемента; б) не более двух элементов.
. Найти вероятность того, что за 10 часов откажут: а) только два элемента; б) не более двух элементов.
Вопросы к защите практической работы №9
1. Какое распределение НВС называется нормальным?
2. Что такое нормированное нормальное распределение НВС?
3. Смысл параметров а и s?
4. Нормальная кривая. Свойства и график нормальной кривой?
5. В чем состоит влияние параметров нормального распределения на форму нормальной кривой?
6. Вероятность попадания в заданный интервал нормально распределенной случайной величины.
7. Как вычисляется вероятность заданного отклонения?
8. В чем состоит правило «трех сигм»?
9. Какое распределение называется показательным?
10. Вероятность попадания в заданный интервал показательно распределенной случайной величины.
11. Числовые характеристики показательного распределения?
12. Что такое функция надежности?
13. В чем состоит показательный закон надежности?
14. Характеристическое свойство показательного закона надежности?
Практическая работа №10
Тема: Элементы математической статистики.
Цель работы: Изучить выборочный метод, числовые характеристики выборки и методику их расчета, точечную и интервальную оценку, методику интервального оценивания математического ожидания нормального распределения при известной и неизвестной дисперсии, методику интервального оценивания вероятности события. Научиться строить графическую диаграмму, рассчитывать числовые характеристики выборки, рассчитывать точечные оценки, доверительные интервалы.






