Биноминальное распределение вероятностей
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, вероятность непоявления q=l-р). Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях.
Поставим перед собой задачу: найти закон распределения величины X. Для ее решения требуется определить возможные значения X и их вероятности. Очевидно, событие А в n испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза,..., либо n раз. Таким образом, возможные значения X таковы: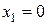 
, 
, 
, …, 
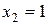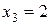. Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли: 
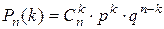, где k=0, 1, 2, …, n.
Формула Бернулли и является аналитическим выражением искомого закона распределения.
Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «биномиальным» потому, что правую часть равенства можно рассматривать как общий член разложения бинома Ньютона:
Таким образом, первый член разложения 
определяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях; второй член определяет вероятность наступления события n—1 раз;...; последний член определяет вероятность того, что событие не появится ни разу.
Напишем биномиальный закон в виде таблицы (см. таблицу 2)
Таблица 2 – Биноминальный закон распределения
| Х | n | n-1 | … | k | … | |
| р |
| 
| … | 
| … | 
|
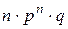
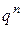
Пример: Монета брошена 2 раза. Составить закон распределения случайной величины Х – числа выпадений «герба».
Решение: вероятность появления «герба» при каждом бросании монеты p =1/2, следовательно, вероятность непоявления «герба» q = 1 – p = 1 – 1/2 = 1/2.
В 2-х испытаниях «герб» может появиться 2 раза, 1 раз или совсем не появиться. Таким образом, возможные значения случайной величины Х: x1 =2, x2 =1, x3 =0. Найдём вероятности этих возможных значений по формуле Бернулли:
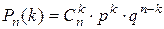
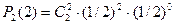= 0,25
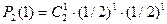= 0,5
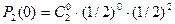= 0,25
Составим закон распределения:
| x | |||
| p | 0,25 | 0,5 | 0,25 |
Распределение Пуассона
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности k появлений события в этих испытаниях используют формулу Бернулли. Если же n велико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала (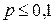
). В этих случаях (n велико, р мало) прибегают к асимптотической формуле Пуассона.
Итак, поставим перед собой задачу найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз. Сделаем важное допущение: произведение 
сохраняет постоянное значение, а именно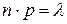 
. Это означает, что среднее число появлений события в различных сериях испытаний, т. е. при различных значениях n, остается неизменным.
Таким образом, получаем формулу:
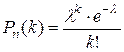, (27)
где 
- общее число испытаний;
- число появлений события А;
- вероятность появления события А в каждом испытании;
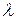- постоянная величина.
Эта формула выражает закон распределения Пуассона вероятностей массовых (n велико) и редких (р мало) событий.
Замечание. Имеются специальные таблицы, пользуясь которыми можно найти 
зная k и .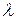
Пример: Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно 5 бракованных книг.
Решение: По условию n = 100 000, k = 5, p = 0,0001. События, состоящие в том, что книги сброшюрованы неправильно, независимы, следовательно имеем схему Бернулли, а т.к. n достаточно велико, а p крайне мало, то воспользуемся распределением Пуассона.
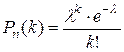
Найдём λ: λ = n∙p = 100 000 ∙ 0,0001 = 10
Искомая вероятность: 
= 0,0375
Так же для нахождения вероятности можно воспользоваться специальными таблицами (приложение Д).
