Пример 1. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна р=0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение: Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна р = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q=1-р=1-0,75=0,25.
Искомая вероятность по формуле Бернулли (15) равна
 .
.
Ответ: Вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы, равна  .
.
Пример 2. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение: По условию задачи n=400; k=80; р=0,2; q=0,8. Воспользуемся локальной формулой Лапласа (18):
 .
.
Вычислим определяемое данными задачи значение х:
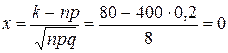 .
.
По таблице приложения А находим
 .
.
Искомая вероятность
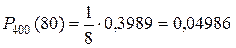 .
.
Ответ: Вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, равна  .
.
Пример 3. Вероятность того, что деталь не прошла проверку ОТК, равна р=0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение: По условию задачи р=0,2; q=0,8; n=400;  =70;
=70;  =100. Воспользуемся интегральной теоремой Лапласа:
=100. Воспользуемся интегральной теоремой Лапласа: 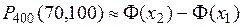 .
.
Вычислим нижний и верхний пределы интегрирования
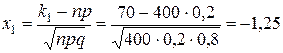 ,
,
 .
.
Таким образом, применяя формулу (20) имеем
 .
.
По таблице приложения Б находим:
Ф(2,5)=0,4938,
Ф(1,25)=0,3944.
Искомая вероятность
 .
.
Ответ: Вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей, равна  .
.
Ход работы
1) Ознакомиться с теоретической частью данной работы (лекции, учебники, данные методические указания).
2) Выполнить задание по своему варианту.
3) Составить отчет по проделанной работе.
4) Ответить на контрольные вопросы к данной работе.
5) Защитить выполненную работу.
Содержание отчета
1) Тема.
2) Цель работы.
3) Ход работы.
4) Решение своего варианта.
Варианты заданий для самостоятельной работы
Вариант 1
1. Играют два равносильных шахматиста. Что вероятнее: выиграть три партии из восьми или две партии из шести.
2. В цехе семь станков. Для каждого станка вероятность того, что он в данный момент работает, равна 0,9. Найти вероятность того, что в данный момент работают три станка.
3. Вероятность того, что изделие не пройдет контроля, равна 0,125. какова вероятность того, что среди 10 изделий не будет ни одного забракованного контролером?
4. Найти вероятность того, что из 600 посеянных семян взойдет 500, если вероятность всхожести 0,95.
5. Вероятность поражения мишени стрелком равна 0,3. Найти вероятность того, что при 2100 выстрелах мишень будет поражена от 600 до 660 раз.
6. Вероятность поражения мишени стрелком при одном выстреле равна 0,8. Найти вероятность того, при 250 выстрелах мишень будет поражена: а) не менее 190 и не более 210 раз; б) не менее 190 раз.
Вариант 2
1. Играют два равносильных шахматиста. Что вероятнее: выиграть четыре партии из семи или две партии из пяти.
2. В классе девять компьютеров. Для каждого компьютера вероятность того, что он в данный момент работает, равна 0,8. Найти вероятность того, что в данный момент работают пять компьютеров.
3. По каналу связи передается 6 сообщений. Каждое из сообщений может быть искажено помехами с вероятностью 0.2 независимо от других. Найти вероятность того, что 4 сообщения из 6 не искажены.
4. Вероятность поражения мишени стрелком равна p = 0,7. Найти вероятность того, что при n = 2100 выстрелах мишень будет поражена ровно 1500 раз.
5. Вероятность того, что саженец ели прижился, и будет расти, равна 0,8. Посажено 400 саженцев ели. Какова вероятность того, что нормально вырастут не менее 250 деревьев?
6. Вероятность появления события в каждом из 400 независимых испытаний постоянна и равна р=0,9. найти вероятность того, что событие появится: а) не менее 350 и не более 370 раз; б) Не более 350 раз.
Вариант 3
1. Играют два равносильных шахматиста. Что вероятнее: выиграть две партии из семи или три партии из восьми.
2. Монету бросают восемь раз. Найти вероятность того, что «герб» выпадет ровно пять раз.
3. В магазине 7 холодильников. Вероятность выхода из строя каждого холодильника в течение года равна 0,2. Найти вероятность того, что в течение года ремонта потребует 4 холодильника.
4. Найти вероятность того, что из 500 посеянных семян взойдет 270, если вероятность всхожести 0,75.
5. Вероятность найти белый гриб среди прочих равна 0,8. Какова вероятность того, что среди 100 грибов белых будет от 75 до 90?
6. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, при 900 выстрелов мишень будет поражена: а) не менее 670 и не более 680 раз; б) не менее 670 раз.
Вариант 4
1. Играют два равносильных шахматиста. Что вероятнее: выиграть три партии из семи или две партии из пяти.
2. В столовой десять столов. Для каждого стола вероятность того, что он занят, равна 0,6. Найти вероятность того, что в данный момент заняты шесть столов.
3. Адвокат выигрывает дело в суде с вероятностью 0,7. Найдите вероятность того, что он из 8 дел выиграет 5.
4. Вероятность поражения стрелком мишени равна p = 0,8. Найти вероятность того, что при n = 100 выстрелах мишень будет поражена ровно k = 86 раз.
5. Вероятность того, что в инкубаторе яйцо вылупится составляет 0,75. Найти вероятность того, что из 100 заложенных в инкубатор яиц вылупится от 70 до 80 яиц.
6. Вероятность поражения мишени стрелком при одном выстреле равна 0,6. Найти вероятность того, при 600 выстрелов мишень будет поражена: а) не менее 350 и не более 370 раз; б) не менее 350 раз.
4.6 Вопросы к защите практической работы №4
1) Какие испытания называются независимыми?
2) Формула Бернулли. Вывод.
3) Когда применяется формула Бернулли?
4) Локальная теорема Лапласа.
5) В каких случаях целесообразно применять теорему Лапласа?
6) Как рассчитать значения функции Лапласа?
7) Интегральная теорема Лапласа.
Практическая работа №5
Тема: Решение задач на запись распределения ДСВ.
Цель работы: Изучить понятие случайной величины, дискретной случайной величины (ДСВ), распределения ДСВ и его графическое отображение, понятие функции от ДСВ. Научиться записывать распределение ДСВ, графически изображать распределение ДСВ, записывать распределение функции ДСВ.






