Специфика методики оценки погрешностей заключается в том, что в данной лабораторной работе используется имитационное моделирование режимов истечения воздуха по заранее заданной программе на ЭВМ. При этом значения расхода воздуха, давлений и температуры на рабочем участке в различных режимах строго фиксированы, измерительная информация снимается с помощью пульта управления и отображается на экране монитора.
При обработке результатов эксперимента на имитационной установке для каждого режима истечения необходимо учитывать класс применяемого измерительного прибора и его допустимые погрешности измерений в соответствии с метрологическими требованиями ГОСТ 8.009-84 и ГОСТ 8.508-86.
При выполнении работы на каждом заданном режиме проводятся однократные измерения расхода, давления и температуры. Порядок расчета при оценке погрешностей рекомендуется следующий.
Определяется класс точности измерительного прибора и оценивается погрешность измерения величины на выбранном диапазоне измерений. Предел допускаемой основной погрешности средства измерения оценивается по формуле
,
где Хп – нормируемое значение измеряемой или определяемой физической величины, g - предел допускаемой погрешности прибора (класс точности прибора).
Определяется предел допустимой погрешности измерения перепада давления DH:
,
где DHк – предел измерения перепада давления; DHх - показания прибора.
Погрешности измерения температуры, барометрического давления и коэффициента расхода сопла принимаются равными 2%.
Предельные отклонения диаметра шайбы и диаметра сопла определяются допусками на изготовление.
Относительная среднеквадратическая погрешность косвенного измерения действительного расхода газа определяется по формуле
.
Контрольные вопросы
1. Перечислите основные положения, на которых базируется теоретическое описание газовых потоков.
2. Запишите основные уравнения, описывающие поведение газовых потоков.
3. Почему невозможно получить давление газа в выходном сечении сопла ниже критического давления?
4. Объясните методику расчета критических параметров в данной работе.
Работа 6 (ММТП-005М)
ИССЛЕДОВАНИЕ ТЕПЛООТДАЧИ ПРИ ВЫНУЖДЕННОМ ДВИЖЕНИИ ВОЗДУХА В ТРУБЕ МЕТОДОМ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ ПРОЦЕССА ТЕПЛООБМЕНА
Цель работы - экспериментально определить локальные и средние по длине трубы значения коэффициента теплоотдачи при вынужденном движении воздуха в трубе при равных скоростях движения и сопоставить результаты опытов с известными критериальными зависимостями.
Введение
Рабочие процессы в различных теплообменных устройствах, как правило, основаны на конвективном теплообмене между твердой поверхностью тела и омывающей его жидкостью (в том числе и газом), а его интенсивность зависит, в первую очередь, от разности температур жидкости и поверхности (температурного напора), а также определяется гидродинамическими условиями обтекания поверхности и теплофизическими свойствами жидкости.
Для расчета теплового потока обычно используют формулу Ньютона, согласно которой плотность теплового потока q пропорциональна температурному напору:
 ,
| 6.1 |
где [q] = 1 Вт/м2 ; a - коэффициент теплоотдачи, [a] = 1 Вт/(м2 К); Т ¦ – температура жидкости вдали от стенки; Тw – температура поверхности теплообмена (стенки).
Современные методы расчета конвективного теплообмена при вынужденном течении основываются на теории пограничного слоя. В непосредственной близости стенки теплота передается только теплопроводностью. Тогда в соответствии с гипотезой Фурье
 .
| 6.2 |
l¦ - теплопроводность жидкости; п – координата, отсчитываемая от нормали к изотермической поверхности.
Если воспользоваться первым приближением производной для теплового пограничного слоя толщины dт
,
то из уравнений (6.1) и (6.2) следует, что
.
Таким образом, для интенсификации теплоотдачи нужно использовать жидкости с высокой теплопроводностью и принимать меры к уменьшению толщины пограничного слоя.
Интенсивность теплоотдачи конвекцией зависит от характера течения жидкости в пограничном слое. При ламинарном режиме течения, когда линии тока не перемешиваются, интенсивность теплоотдачи невелика, слабо зависит от скорости течения и сильно изменяется при изменении теплофизических свойств теплоносителя.
При турбулентном режиме течения скорость в каждой точке потока пульсирует около некоторого среднего по времени значения. Вследствие этого возникает интенсивное поперечное перемешивание жидкости, что и вызывает интенсивный обмен количеством движения и теплотой между слоями с различной скоростью. При вынужденном течении жидкости в трубах только на достаточном удалении от входа, когда толщина пограничного слоя становится равной радиусу трубы, устанавливается устойчивое распределение скорости и температуры по сечению (стабилизированное течение), не зависящее от начальных условий.
На начальном участке, где имеет место нестабилизированное течение, процесс теплоотдачи отличается большой сложностью, и коэффициент теплоотдачи резко изменяется по величине.
Распределение температуры и скорости для несжимаемой жидкости с постоянными физическими свойствами описывается системой дифференциальных уравнений, которые в приближении стационарного двумерного пограничного слоя имеют вид:
уравнение энергии
 ,
| 6.3 |
уравнение движения
 ,
| 6.4 |
уравнение неразрывности
 .
| 6.5 |
В этих уравнениях r - плотность жидкости; Ср – теплоемкость при постоянном давлении; l - теплопроводность; g – ускорение свободного падения; m - динамическая вязкость; Х, Y – ортогональная продольная и поперечная координаты соответственно. Wx, Wу – продольная и поперечная составляющие скорости соответственно; Т – термодинамическая температура; 
– температурный напор.
Система уравнений (6.3) – (6.5) описывает бесчисленное множество процессов конвективного теплообмена. Частные особенности процессов теплообмена характеризуются условиями однозначности, которые содержат геометрические, физические, временные и граничные условия. Коэффициент теплоотдачи a, как следует из анализа системы дифференциальных уравнений и условий однозначности, является сложной функцией, зависящей от большого числа факторов. Так, например, в случае внутренней задачи (течение жидкости в трубе)
 .
| 6.6 |
Здесь х – расстояние от входа в трубу; Wср – среднемассовая скорость течения жидкости; d – диаметр трубы; l – длина трубы.
При аналитическом решении задачи искомая величина (коэффициент теплоотдачи a, температура Т и т.п.) выражается в функции аргументов независимых переменных (время t, координаты х, у, z) и параметров системы (m, u, l,r).
Однако во многих случаях математическое описание процессов теплообмена оказывается настолько сложным, что решить задачу аналитически не представляется возможным. В этих случаях задача может быть решена либо численным методом, либо экспериментально. Оба метода позволяют найти решение лишь для одного конкретного случая. При изменении хотя бы одного параметра задачу необходимо решать заново.
При большом количестве аргументов объем вычислений или экспериментов оказывается очень большим; кроме того, чрезвычайно трудной задачей становится подобрать эмпирическую зависимость, правильно отражающую влияние всех аргументов, то есть обобщить результаты численных решений или экспериментов. Эти трудности преодолеваются с помощью так называемых обобщенных переменных или критериев подобия, представляющих собой безразмерные комплексы физических величин.
Структура критериев подобия может быть найдена либо на основе анализа дифференциальных уравнений, описывающих явление и содержащих общие связи между величинами (метод теории подобия), либо на основе анализа размерностей физических величин, существенных для явления (метод анализа размерностей). По физическому смыслу критерии подобия выражают соотношения между физическими эффектами (силами, тепловыми потоками).
Критерии подобия, состоящие из физических величин, заданных условиями однозначности, называются определяющими. Критерии, содержащие неизвестные (искомые) величины, называются определяемыми.
Зависимости между критериями подобия называются критериальными уравнениями и, как следует из вышесказанного, находятся с помощью экспериментов или численных решений.
Для конвективного теплообмена в каналах основными критериями подобия являются:
критерий Нуссельта
 ,
| 6.7 |
характеризующий отношение между потоком теплоты от жидкости к поверхности тела (теплоотдачей) и потоком теплоты теплопроводностью в жидкости у стенки; l - теплопроводность жидкости;
критерий Рейнольдса
 ,
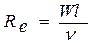| 6.8 |
характеризующий отношение между инерционной силой и силой внутреннего трения в жидкости (вязкости). В критерии Рейнольдса W – среднемассовая продольная скорость жидкости; l – характерный размер (для круглых труб l=d); n - кинематическая вязкость жидкости;
критерий Прандтля
 ,
| 6.9 |
характеризующий совокупное отношение между силами инерции и вязкости и потоками теплоты – конвективным и вынужденным. Для газов критерий Pr определяется только атомностью и его значение близко к единице. Величина а является температуропроводностью среды;
критерий Пекле
 ,
| 6.10 |
характеризующий отношение между потоком теплоты, переносимым движущейся жидкостью (конвективным), и потоком теплоты теплопроводностью при одинаковом температурном напоре;
критерий Грасгофа
 ,
| 6.11 |
характеризующий отношение между подъемной силой в жидкости, возникающей вследствие разности плотностей, и силой вязкости. В (6.11) b - коэффициент объемного расширения жидкости; DT - разность температур жидкости и стенки.
В случае вынужденной конвекции при течении жидкости в трубах и каналах анализ методами теории подобия приводит в общем случае к функциональной связи:
 ,
| 6.12 |
где l/d – отношение длины трубы к ее диаметру, учитывающее изменение теплоотдачи по длине трубы на начальном участке. При ламинарном режиме течения (если 
) в общем случае на теплоотдачу при вынужденном движении оказывает влияние свободная конвекция, что и учитывается введением в число независимых аргументов критерия Gr. Однако влияние свободной конвекции на теплоотдачу ощущается лишь в том случае, когда имеет место так называемый вязкостно-гравитационный режим течения теплоносителя (
). В остальных случаях влиянием свободной конвекции пренебрегают, и функциональная зависимость (6.12) принимает вид:
 .
| 6.13 |
При развитом турбулентном режиме течения (Re ³ 104) общий вид функциональной зависимости остается тем же. Экспериментальные данные по теплоотдаче при вынужденной конвекции обычно обобщают в виде степенной зависимости
 .
| 6.14 |
Критериальное уравнение для определения коэффициента теплоотдачи a при вынужденном квазиизотермическом 
турбулентном течении жидкости 
на основном участке трубы (участке стабилизированного течения) имеет вид
 .
| 6.15 |
При меньших значениях числа Re¦, то есть в переходной области течения (2300 £ Ref £104) теплоотдача может быть рассчитана по уравнению
 ,
| 6.16 |
где ¦(Re¦) – функция, зависящая от Re¦.
Таблица 6.1
| 
| ||||||||||
| 3.6 | 4.9 | 7.5 | 12.2 | 16.5 | 0.021× 
|
При течении жидкости на начальном участке трубы динамический и тепловой пограничные слои еще не сомкнулись, то есть происходит формирование профилей скорости и температуры. При этом коэффициенты теплоотдачи и гидравлического сопротивления являются функцией расстояния от входного сечения канала.
При постоянной по длине трубы плотности теплового потока (
) и ламинарном течении коэффициент теплоотдачи на начальном участке падает ввиду увеличения толщины пограничного слоя.
При турбулентном течении процесс стабилизации движения и теплообмена происходит быстрее, чем при ламинарном. В условиях гидродинамической стабилизации газового потока длина участка тепловой стабилизации соответствует l/d = 20 …30.
