Цель работы -экспериментально определить коэффициент излучения электропроводящего материала в зависимости от температуры и характеристик поверхностей (шероховатости и степени окисления).
Введение
Все нагретые тела излучают энергию в виде электромагнитных волн, распространяющихся в вакууме со скоростью света 
. От длины волны зависит действие излучения при падении его на вещество (табл.2.1).
Таблица 2.1. Шкала электромагнитных волн
| Виды излучения | Длина волны излучения l, м |
| Космическое (корпускулярное) g - излучение Рентгеновское Ультрафиолетовое Видимое Тепловое (инфракрасное) Электромагнитные волны | < 0.05·10-12 0.05·10-12 ¸ 0.1·10-12 1·10-12 ¸ 20·10-9 20·10-9 ¸ 0.4·10-6 0.4·10-6 ¸ 0.8·10-6 0.8·10-6 ¸ 0.8·10-3 0.2·10-3 ¸1·103 |
Процесс распространения электромагнитных волн, испускаемых телом в некоторой области пространства, совершенно не зависит от температуры окружающей среды. В этом его главное отличие от теплового потока теплопроводности и конвекции, возникновение которых связано с градиентом (перепадом) температуры.
Множество твердых и жидких тел излучают энергию всех длин волн, т.е. имеют сплошной спектр излучения с l от 0 до ¥. К таким телам относятся материалы с окисленной шероховатой поверхностью. Диэлектрики (непроводники электричества), полупроводники с кристаллической структурой имеют четкие линии излучения и поглощения. Чистые металлы с полированной поверхностью, газы и пары излучают энергию дискретно в определенных интервалах длин волн, т.е. имеют прерывистый спектр. Твердые и жидкие тела имеют значительные поглощательную и излучательную способности. Эти процессы у них протекают в тонких поверхностных слоях.
Интенсивность излучения зависит от природы тела, его теплового состояния (температуры), длины волны, состояния поверхности, а для газов и паров еще от толщины слоя и давления, так как их излучение и поглощение осуществляются всеми частицами объема вещества.
Процесс лучистого теплообмена между телами – это процесс превращения тепловой энергии в лучистую, и обратно. Лучеиспускание свойственно всем телам при температурах, отличных от абсолютного нуля. Количество энергии излучения, передаваемое в единицу времени через произвольную поверхность Q [Вт], называется потоком излучения (различают монохроматический и интегральный потоки излучения). Из энергии излучения Q0, которая падает на тело в результате излучения других тел, часть QA поглощается телом, часть QR отражается, часть QD проходит сквозь него, следовательно,
 .
| 2.1 |
Обозначим А, R, D - поглощательную, отражательную и пропускательную способности тела соответственно: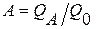 
; 
; 
:
 .
| 2.2 |
Абсолютно черное тело поглощает всю падающую на него энергию (А=1). Если поглощательная способность 
, не зависит от температуры и определяется длиной волны («цветом»), то тело называется серым. Абсолютно белое тело полностью отражает все падающее излучение - 
, абсолютно прозрачное (диатермичное) все пропускает - 
. В природе не существует идеальных тел.
Введение в рассмотрение процессов идеальных тел необходимо, поскольку они дают предельные значения свойств, которые не достижимы реальными телами. Так, при переносе теплоты излучением между реальными телами для каждого из них
 ,
| 2.3 |
но в общем случае справедливо соотношение (2.2).
Значения А, R и D зависят от природы тела, состояния поверхности, температуры и длины волны излучения. Например, обычное стекло пропускает видимые лучи и является непроницаемым для ультрафиолетовых лучей и в очень малой степени проницаемо для тепловых лучей.
Законы теплового излучения получены применительно к идеальному абсолютно черному телу в термодинамическом равновесии с окружающей средой (см. ВВЕДЕНИЕ). Равновесным тепловым излучением называют тепловое излучение тел в замкнутой изотермической системе. Тепловое излучение имеет динамический характер. Тела в равновесной термодинамической системе одновременно излучают и поглощают энергию в одинаковых количествах, а результирующий поток энергии равен нулю (
).
Отношение плотности потока излучения, испускаемого в бесконечно малом интервале длин волн, к величине этого интервала длин волн называется спектральной плотностью потока излучения Е l. Зависимость спектральной плотности потока излучения от длины волны и температуры для абсолютно черного тела устанавливается законом Планка:
 ,
| 2.4 |
где Е0l - спектральная плотность потока излучения (спектральная интенсивность излучения) абсолютно черного тела, [Е0l] =1 Вт; С1 = 3.74·10 –16 [Вт/м2]и С2 = 1.438·10-2 [м.К] – постоянная закона Планка; l - длина волны [м], Т – абсолютная температура. Закон Планка получен для абсолютно черного тела, для нечерных тел он выражает максимально возможную плотность потока излучения.
| Излучение абсолютно черного тела имеет непрерывный спектр и зависит только от температуры и длины волны. При малых и очень больших длинах волн  и  спектральная плотность излучения стремится к нулю. С повышением температуры максимум  смещается к коротким длинам волн. Спектральная плотность потока излучения Е0l имеет свое максимальное значение при каждой температуре излучения (рис.2.1).
|
| Рис.2.1. Спектры излучения абсолютно черного тела |
Длина волны lmах, на которую приходится максимум при данной температуре Т определяется следующим образом:
 .
| 2.5 |
Соотношение (2.5) составляет содержание закона Вина. Пользуясь уравнением (2.5), можно вычислить температуру тела по распределению интенсивности в его спектре, рассматривая тело как черное или серое. Например, для Солнца lm»0.48 [м.К], что отвечает температуре его поверхности Т» 6000 [К].
Закон Стефана-Больцмана устанавливает зависимость плотности потока интегрального полусферического излучения абсолютно черного тела Е0 от температуры:
 .
| 2.6 |
Здесь Е0 – плотность потока интегрального полусферического излучения абсолютно черного тела [Вт/м2], С0 – коэффициент излучения абсолютно чер-
| ного тела С0 = 5.6687 [Вт/м2 К4 ], Т – абсолютная температура тела. Закон Стефана-Больцмана строго справедлив для серого излучения (рис.2.2).
Спектральная плотность излучения для каждого серого тела Еl составляет некоторую и притом одинаковую для всех длин волн и температур долю от спектральной плотности излучения Е0l абсолютно черного тела, то есть
 (2.7)
|
| Рис. 2.2- Плотность потока излучения в зависимости от длины волны при одинаковой температуре. 1 – абсолютно черное; 2 – серое; 3 – селективное излучение (спектр) |
Величина el называется спектральной степенью черноты (спектральная относительная испускательная способность), численное значение которой зависит от физических свойств, качества поверхности того или иного серого тела.
Очевидно, что согласно условиям, определяющим серое излучение, спектры излучения серого и абсолютно черного тел при одинаковых температурах подобны друг другу, а интегральная степень черноты e равна спектральной el:
 и  .
| 2.8 |
Закон Стефана-Больцмана для определения плотности потока интегрального полусферического излучения серого тела записывается в виде:
 .
| 2.9 |
где С=eС0 - коэффициент излучения серого тела, [ С ]= 1 [Вт/(м2·К4)]. Сопоставляя энергии интегрального излучения серого и абсолютно черного тела (2.8), степень черноты e серого тела можно представить через отношение коэффициентов излучения:
 .
| 2.10 |
Значение e для серых тел лежит в пределах от 0 до 1, а коэффициента излучения - от 0 до 5.6687 [Вт/(м2К4)].
Как показали опыты, большинство технических материалов (непроводники и полупроводники электричества, металлы в окисленном состоянии) в достаточной степени проявляют свойства серого тела. Применение закона Стефана-Больцмана к реальным телам, принимаемым за серые тела, является справедливым лишь в той мере, в какой можно допустить, что коэффициент излучения постоянен и не зависит от температуры. В действительности коэффициент излучения (степень черноты) этих тел определяется не только его природой и температурой излучающей поверхности, но и ее состоянием. С увеличением шероховатости поверхности величина e заметно возрастает. Так, например, для тщательно полированной электролитной меди e = 0.018, а для продолжительно нагревавшейся, покрытой тонким слоем окиси, e = 0.78.
Коэффициент излучения или степень черноты в большинстве случаев определяются экспериментально. В отличие от серых тел, тела с селективным излучением (рис.2.2) могут излучать и поглощать энергию в определенных, характерных для каждого тела областях спектра.
Закон Кирхгофа устанавливает связь между свойствами тела как поглотителя энергии, и как излучателя ее и формулируется так: отношение лучеиспускательной способности тела к поглощательной способности одинаково для всех тел, находящихся при одной и той же температуре, и равно лучеиспускательной способности абсолютно черного тела при той же температуре.
 
| 2.12 |
Степень (коэффициент) черноты e какого-либо тела во всем интервале черного излучения равна поглощательной способности того же тела при той же температуре.
Для монохроматического излучения для каждой длины волны в отдельности
 и .
| 2.13 |
Отношение спектральной плотности излучения какого-либо тела при определенной длине волны к его поглощательной способности при той же длине волны одинаково для всех тел, находящихся при одной и той же температуре, и равно спектральной плотности излучения абсолютно черного тела при той же температуре и длине волны. Из закона Кирхгофа следует, что поскольку
| величина поглощательной способности А лежит в интервале между 0 и 1, то лучеиспускательная способность всех тел меньше, чем лучеиспускательная способность абсолютно черного тела. Лучеиспускательная способность тел тем больше, чем выше их поглощательная способность. Задачу лучистого теплообмена между телами можно решать по-разному. Например, используя метод эффективных потоков излучения тел, или метод многократных отражений. |
| Рис.2.3 – Распределение лучистых потоков для D=0; A+R=1. |
Рассматривая процесс лучистого теплообмена (рис.2.3) видно, что для непрозрачных тел (D=0; A+R =1) эффективное излучение тела равно сумме плотностей потоков собственного и отраженного излучения, то есть
 .
| 2.14 |
Результирующая плотность потока излучения 
между телом и окружающей его средой представляется разностью между эффективными плотностями встречных потоков.
 .
| 2.15 |
Эффективное излучение – это излучение тела, которое мы ощущаем или измеряем приборами; оно больше поглощенного на величину 
. Физические качества собственного и отраженного излучений неодинаковы, а их спектры различны. Для тепловых расчетов это различие не имеет значения, ибо здесь рассматривается лишь энергетическая сторона процесса. Этот способ определения результирующей плотности потока излучения балансирует приборные показания (например, радиометров) (2.15) и не требует знания ни температуры, ни лучеиспускательных способностей окружающих тел системы для определения энергии падающего излучения.
Метод многократных отражений требует знания температур излучения и лучистых свойств тел при использовании закона Стефана-Больцмана в конкретной геометрической системе.
| Определим результирующий лучистый поток Q1,2 системы двух серых тел, концентрически расположенных сфер, разделенных сферическим вакуумированным пространством (рис.2.4). Сферы – внутренняя 1 и внешняя (оболочка) 2 имеют постоянные температуры Т1 и Т2, коэффициенты поглощения А1 и А2 во всех точках своих поверхностей F1 и F2. |
| Рис.2.4 |
При Т1>Т2 результирующий поток Q1,2 определяется разностью между лучистым потоком, поглощенным телом 2, при излучении тела 1 Q1®2, и потоком, поглощенным телом 1 при излучении тела 2 Q2®1:
 .
| 2.16 |
В данном случае на первую поверхность попадает лишь некоторая часть энергии, излучаемой второй поверхностью, которая учитывается коэффициентом j2,1, остальное количество проходит мимо и снова попадает на вторую поверхность. Коэффициент j2,1 называется угловым коэффициентом излучения. Угловой коэффициент j1.2 =1 так как энергия, излучаемая первым, всюду выпуклым телом, целиком попадает на второе тело, то есть j 1,1=0; j 2,2=1-j2,1. Рассмотрим последовательность движения лучистого потока, испускаемого телом.
С единицы поверхности тела 1 излучается поток Е1, единица поверхности 2 поглощает поток Е1А2 и отражает поток 
. Тело 1 поглощает поток 
, который определяется угловым коэффициентом j2,1 и поглощательной способностью А1, и отражает к телу 2 поток 
. В свою очередь, тело 2 поглощает лучистый поток 
и отражает поток 
. Из этого количества энергии тело 1 поглощает 
и отражает 
и т.д. Анализ процесса излучения тела 2 на тело 1 может быть проведен аналогичным образом.
Если принять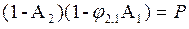 
, то лучистый поток, поглощаемый телом 2 при излучении только тела 1, будет
| 2.17 |
Так как 
, то сумма бесконечно убывающей прогрессии
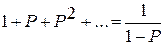
| 2.18 |
Тогда
 .
| 2.19 |
Лучистый поток, поглощаемый телом 1 при излучении телом 2,
 .
| 2.20 |
Результирующий поток в системе двух серых концентрических сфер согласно (2.16) будет равен
.
Умножая на 
правую часть равенства и учитывая (2.18), имеем:
 .
| 2.21 |
Предположим, что Т1=Т2, тогда результирующий поток Q1,2 =0, а так как e =А (2.12), получим, что средний угловой коэффициент излучения зависит от геометрических характеристик излучающей системы:
 .
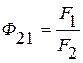| 2.22 |
После подстановки в (2.21) формула результирующего лучистого потока примет вид
 .
| 2.23 |
где 
- приведенный коэффициент поглощения системы тел 1- 2.
Так как для серых тел степень черноты e =А=С/С0, то
 .
| 2.24 |
где 
- приведенный коэффициент излучения системы тел 1-2 [ Вт/(м2К4)], С1 и С2 – коэффициенты излучения.
Формулы (2.23) и (2.24) применимы для произвольных невогнутых тел с оболочкой, а также для случая, когда выпуклое тело 1 и вогнутое тело 2 образуют замкнутое пространство. В этих случаях угловой коэффициент излучения j2,1 имеет смысл среднего углового коэффициента.
Эти же выражения можно использовать для расчета других систем – двух параллельных поверхностей (F1=F2=F), у которых высота и длина несопоставимо велики по сравнению с расстоянием между ними. Для участков, удаленных от торцов, где доля потерь лучистой энергии ничтожна, а этом случае j1,2 =j2,1=1 и выражения (2.23) и (2.24) примут вид
 .
| 2.25 |
где 
; 
.
Применив формулу (2.24) к центральному, только выпуклому цилиндрическому телу 1 с оболочкой 2, когда F1 << F2, будем считать, что j2,1®, тогда Сп ® С1, откуда получим
 .
| 2.26 |
Приведенное выражение (2.26) легло в основу экспериментального определения коэффициента С1 излучающей поверхности электропроводящего материала центрального тела 1.
Задача состоит в экспериментальном исследовании зависимостей коэффициентов излучения и степени черноты поверхности вольфрамовой проволоки от температуры, а также определение коэффициента излучения меди в зависимости от качества излучающей поверхности.
