Прежде чем перейти к построению схем компараторов, необходимо вспомнить порядок построения схем, реализующих функции «Равнозначность» и «Неравнозначность» (см. п.2.3.2).
Составим функции «Равнозначность» и «Неравнозначность», которые будем использовать в дальнейшем. Функция «Равнозначность» принимает значение 1, если две ее входные переменные имеют одинаковые логические потенциалы: x1=x2=1 ИЛИ x1=x2=0. Поэтому ее представляют как 
. Условное изображение элемента «Равнозначность» приведено на рис.3.17,а.
Рис.3.17. Условные изображения элементов «Равнозначность» (а) и «Неравнозначность» (б).
Функция «Неравнозначность» принимает значение 1, если две ее входные переменные имеют разные логические потенциалы: x1=1, x2=0 ИЛИ x1=0, x2=1. Поэтому ее представляют в следующем виде:
,
где значок 
- символизирует функцию «Неравнозначность».
Функцию «Неравнозначность» иначе называют «Исключающее ИЛИ». Ей присуще интересное свойство: если на один ее вход подать лог.1, то логический потенциал, поданный на второй вход, будет на выходе инвертирован; если же вместо лог.1 на один вход подать лог.0, то функция будет вести себя как повторитель логического потенциала, поданного на другой вход. Это легко проверит это самостоятельно. Условное изображение элемента «Неравнозначность» дано на рис.3.17,б. Вместо приведенного значка (=1) используется значок m2, указывающий на то, что «Исключающее ИЛИ» функционирует по правилам сложения одноразрядных двоичных чисел (сложение по модулю 2): 1+0=1; 0+1=1; 0+0=0; 1+1=0 (при арифметическом сложении единица переносится в соседний более старший разряд).
Пример 3.3. Построить схему сравнения чисел с использованием элементов «Равнозначность» и базисных логических элементов.
Решение.
Остановимся подробнее на равенстве чисел. Заметим, что функция Fa=b — функция «Равнозначность». По смыслу она противоположна функции 
«Неравнозначность» («Исключающее ИЛИ»):
, т.е. 
.
Поэтому проверку равенства одноименных разрядов двух чисел можно осуществить, используя элемент «Равнозначность» (рис.4, а).
Два многоразрядных числа A и В равны, если их одноименные разряды содержат одинаковые цифры (а0=b0 И а1=b1 И... И аn-1=bn-1), т.е. функция, характеризующая соотношение чисел, должна быть конъюнкцией функций, характеризующих соотношение цифр в их одноименных разрядах:
.
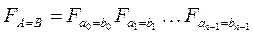Когда цифры в одноименных разрядах чисел А и В одинаковы, то на выходах всех элементов «Равнозначность» стоят лог.1 и FA=B=1 (см.рис.3.18). Если хотя бы в одной паре разрядов находятся разные цифры, то на выходе соответствующего элемента «Равнозначность» будет лог.0, и функция FA=B=0, что указывает на неравенство чисел А и В.
Рис.3.18. Схема сравнения двух чисел на базе
элемента «Равнозначность»
Построение схем сравнения (компараторов) для неравенства чисел. Рассмотрим теперь неравенство чисел, используя выражение
; 
; 
. (3.5)
Пусть А>В. Выявление такого неравенства начинается со старших разрядов; если они равны, то сравнивается следующая пара одноименных разрядов и т. д. Так, в случае 3-разрядных чисел могут быть следующие варианты:
1) неравенство цифр в старших разрядах (а2>b2), что в соответствии с (1) представляется выражением 
. При этом неравенство чисел А>В описывается тем же выражением;
2) равенство цифр в старших разрядах (а2=b2), что представляется выражением (
) и неравенство цифр в средних разрядах чисел (а1>b1), что описывается выражением 
. При этом неравенство чисел А>В представляется конъюнкцией двух приведенных выражений 
.
3) равенство цифр в старших и средних разрядах (а2=b2, а1=b1), что описывается выражениями 
и 
, и неравенство цифр в младших разрядах (a0>b0), что описывается выражением 
. При этом неравенство чисел А>В представляется конъюнкциями трех предыдущих выражений 
.
Пример 3.4. Построить схему на основе базисных логических элементов для сравнения многоразрядных чисел.
Поскольку возможен любой из трех вариантов, то выражение, учитывающее все варианты, запишется в виде дизъюнкции приведенных конъюнкций:
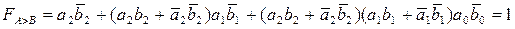. (3.6)
Если на выходе схемы, элементы которой реализуют приведенные конъюнкции и дизъюнкцию из выражения (3.6), устанавливается лог.1, то число А>В. Этому соответствует схема, приведенная на рис.3.19.
Рис. 3.19. Схемы сравнения определения А>В
По аналогичным схемам (см. рис.5б) выполняются компараторы для сравнения чисел с большей разрядностью.
