Логическая функция может быть записана аналитически различными сочетаниями операций сложения и умножения переменных. Однако с точки зрения представления логической функции и последующего синтеза логической схемы наиболее удобны формы записи, при которых функция выражается либо в виде суммы произведений переменных, либо в виде произведения их сумм.
Запись логической функции в виде суммы произведений переменных называют дизъюнктивной нормальной формой (ДНФ):

а запись функции в виде произведения сумм — конъюнктивной нормальной формой (КНФ):
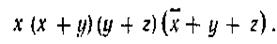
Инверсия любой функции, записанной в дизъюнктивной (конъюнктивной) нормальной форме, по правилу (1.5) дает замену записи на конъюнктивную (дизъюнктивную) нормальную форму. Например, инверсия функции

имеет вид
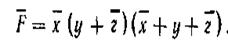 .
.
Логическую функцию, заданную любым аналитическим выражением, можно преобразовать к ДНФ или КНФ, пользуясь правилами алгебры логики. Для каждой логической функции может существовать несколько равносильных дизъюнктивных и конъюнктивных форм.
Вместе с тем имеется только один вид ДНФ и КНФ, в которых функция может быть записана единственным образом (совершенные нормальные формы). В совершенной дизъюнктивной нормальной форме (СДНФ) каждое входящее слагаемое включает все переменные (с инверсиями и без них) и нет одинаковых слагаемых. В совершенной конъюнктивной нормальной форме (СКНФ) каждый входящий сомножитель включает все переменные (с инверсиями и без них) и нет одинаковых сомножителей.
Логическая функция наиболее наглядно и полно представляется так называемой таблицей соответствия или истинности, в которой для каждой комбинации значений переменных указывается значение функции. Таким образом, таблица истинности определяет алгоритм работы создаваемой цифровой схемы. От табличного представления функции переходят к аналитической записи ее в СДНФ или СКНФ.
Пусть в качестве примера функция F задана в виде табл.2.3. Для комбинаций переменных 2, 7, 8 функция F истинна (т. е. F=1), что означает для указанных комбинаций равенство единице следующих произведений: хуz=1.
Таблица 2.3
Таблица истинности
| Номер комбинации | X | Y | Z | F |
Комбинации переменных, при которых функция истинна, называют конституентами единицы или минтермами. Представление логической функции в виде суммы минтермов определяет ее СДНФ, т. е. в данном случае: 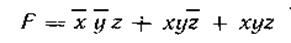 .
.
Функция, определяемая таблицей истинности, может быть представлена не только ее единичными, но и нулевыми значениями. Так, на основании табл.2.3 рассматриваемая функция ложна (F =0 или F=1), если истинно каждое из произведений
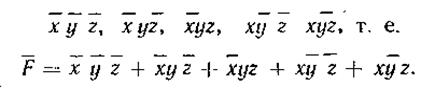
Воспользовавшись законом инверсии, приходим к записи функции в СКНФ:

Каждый сомножитель в этом соотношении состоит из суммы переменных, для которых функция обращается в нуль в соответствии с таблицей истинности. Такие суммы называют конституентами нуля или макстермами. Таким образом, произведение макстермов определяет СКНФ функции.






