Замечание. Устойчивость относительной частоты представляет собой одну из простейших и в то же время основных закономерностей, проявляющихся в сфере «случайного». В дальнейшем все основные (их всего 3) формулы теории вероятностей (из которых следует все формулы этой теории, включая самые сложные) мы получим исходя из этой закономерности.
Устойчивость частот – это объективное свойство массовых случайных явлений окружающего нас реального мира. Отсутствие устойчивости частот в сериях испытаний свидетельствует о том, что условия, при которых производятся испытания, претерпевают значительные изменения (другими словами мы проводим разные опыты).
Таким образом, теория вероятностей является математической моделью окружающего нас (реального) мира в сфере «случайного».
Замечание. Приведённое выше определение вероятности наилучшим образом соответствует потребностям приложений и отражает объективный характер вероятности. Другими словами, если найденная путем некоторого расчета (по формулам теории вероятностей) вероятность события А равна числу p, то реальная ценность этого результата состоит прежде всего в возможности такого предсказания: при большом числе опытов относительная частота наступления события А будет близка к p.
Алгебра событий
При нахождении вероятностей приходится учитывать связи между событиями. Наиболее простые из них заключаются в том, что одни события являются комбинациями других. Рассмотрим три вида основных комбинаций: сумма событий, произведение событий, переход к противоположному событию.
Пусть с некоторым опытом связаны события А и В.
1. Сумма событий. Суммой (или объединение) событий А и В назовём событие, обозначаемое А+В (или А 
В), которое наступает тогда и только тогда, когда наступает или событие А или событие В (или оба вместе).
2. Произведение событий. Произведением (или пересечением) событий А и В назовём событие, обозначаемое AB (или 
), которое считается наступившим тогда и только тогда, когда наступают оба события А и В. Другими словами, АВ есть совместное наступление событий А и В.
Противоположное событие. Событие назовём событием, противоположным к событию А, если оно наступает тогда и только тогда, когда событие А не наступает.
Равенство событий. События А и В считаются равными, если всякий раз, когда наступает одно из них наступает и другое.
Замечание. Чаще всего равные события имеют отличающиеся по форме словесные описания. Например, событие «не все студенты данного курса успешно сдали экзамен по теории вероятностей» и событие «по крайней мере один из студентов данного курса не сдал теорию вероятностей» равны, хотя и выражены различными оборотами речи.
Пример 1. Опыт заключается в бросании игральной кости. При бросании может выпасть число очков, равное какому либо числу из множества чисел {1,2,3,4,5,6}. Рассмотрим в этом случае следующие события:
А = {выпадение чётного числа очков}
В = {выпадение нечётного числа очков}
С = {выпадение числа очков больше трех}
Тогда.
А+В = {выпадение числа очков равное или 1, или 2,..., или 6}= - достоверное событие
А+С = {выпадение числа очков, равное или 2 или 4 или 5 или 6}
АВ = Ø - невозможное событие
АС = {выпадение числа очков равное или 4 или 6}
= {выпадение нечётного числа очков}= В.
Пример 2. Этот пример важен для наглядного истолкования соотношений между событиями. В некоторую область D на плоскости (например квадрат) случайно бросается точка. В этом случае каждое событие рассматривается как попадание случайно брошенной точки в некоторую область D 1 области D. Иначе говоря, каждое событие задаётся некоторой фигурой в области D. При таком истолковании событие А+В будет, не что иное, как попадание точки в область, являющуюся объединением фигур А и В (рис.1), событие АВ - попадание в область, являющуюся пересечением фигур А и В, а событие – попадание в область дополнительную к фигуре А (на рис. 1, соответствующие области заштрихованы)
Событие А = {попадание точки в круг А }
Событие В = {точка попадает в треугольник В }
Беря несколько событий А, В, С, D, … и применяя к ним в любом порядке операции сложения, умножения, переход к противоположным событиям, можно строить различные комбинации, например: 
.
Укажем наиболее важные свойства операций над событиями.
Первые две формулы (формулы де Моргана) являются основными, они связывают сразу все три операции.
1. 
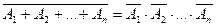- дополнение до суммы есть произведение дополнений
2. 
- дополнение до произведения есть сумма дополнений
3. 
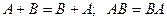- коммутативность
4. 
- ассоциативность
5. 
- дистрибутивность
6. 
7. 
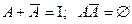
Задачи:
1. Показать, что: 
2. Электрическая цепь составлена по схеме приведённой на рисунках. События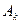 
= (элемент с номером к не вышел из строя (другими словами ток через этот элемент проходит). Событие A = (цепь работает). Выразить событие А через события .
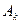3. При условии задачи №2. Событие 
= (элемент с номером к вышел из строя), событие В = (разрыв цепи). Выразить событие В через события .
События А и В называются несовместными, если они не могут наступить вместе в одном опыте, т.е. если 
.
Говорят, что события 
образуют полную группу событий, если они попарно несовместны и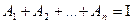 
(т.е. при осуществлении опыта хотя бы одно из этих событий наступит).
Другими словами, если события - образуют полную группу событий, то в результате каждого опыта обязательно наступает одно и только одно из событий .
