Программа «Школа 2000» (Л.Г. Петерсон)
Урок 5
Ход урока
У: Ребята, мы с вами на предыдущих занятиях поставили цель: научиться делить любое многозначное число на многозначное, и сегодня мы сделаем еще один шаг на пути к этой цели.
Для этого мы вспомним, что мы уже умеем делать.
У: Я показываю выражения на деление, вы на пальцах показываете, сколько цифр будет в частном.
(по ходу учитель отделяет выражения с однозначным частным)
487: 31, 2742: 86, 9350: 847, 16844: 8422, 2696: 674, 1350: 225
Дети объясняют по просьбе учителя способ.
У: Какие выражения я оставила?
Д: С однозначным частным.
У: Выполните прикидку частного в каждом случае (по колонкам). Найдите частное.
Д: 2 896: 674» 2 400: 600 = 4, 647 • 4 = 2 696
16 844: 8 422» 16 000: 8 000 = 2, 8 422 • 2 = 16 844
1 350: 225» 14 000: 200 = 7, 225 • 7 = 1 575, 225 • 6 = 1 350, подойдет 6.
У: Откройте тетради, запишите число. Выполните деление в тетради:
504: 84
218: 35
Кому трудно, смотрите образец (с.31).
У: Положили ручки. Проверяем (1 ученик отвечает с места. а учитель записывает).
Д: 504: 84» 480: 80 = 6
84 • 6 = 504
504: 84 = 6
Д: 218: 35» 210: 30 = 7
35 • 7 = 245 - не подходит
35 • 6 = 210 – не подходит
У: Какие проблемы возникли при решении 2-го примера?
У: Чем он отличается от 1-го?
Д: Там не будет целого частного. Там будет остаток.
У: Так чему мы будем учиться на уроке?
Д: Учиться делить с остатком, когда в частном однозначное число.
У: Да. Для этого мы попробуем решить более простой пример на деление с остатком: 84: 39
У: Выполните прикидку частного.
Д: 80: 40 = 2
У: Выполните проверку.
Д: 39 • 2 = 78 - не подходит
39 • 3 = 118 – не подходит
У: Какое самое большое частное?
Д: 2.
У: 84: 39 = 2.
У: Какое число мы разделим?
Д: 39 • 2 = 78
У: Какое число осталось разделить?
Д: 84 – 78 = 6
У: Как называется число 6?
Д: Остаток.
У: 84: 39 = 2 (ост.6)
У: Что мы знаем про остаток?
Д: Остаток меньше делителя: 6<39.
У: Это можно записать в столбик. Кто умеет, как? Кто у доски запишет?
Д: (1 ученик) 84 I _39
78 2
У: Теперь вернемся к нашему частному
218: 35» 210: 30 = 7
35 • 7 = 245
35 • 6 = 210
Кто уже может в строчку записать ход решения?
Д: 218: 35 = 6 (ост.8) 8<35
218 I _35
210 6
|
Учитель задает вопросы по образцу: Кто объяснит решение, пользуясь образцом?
У: Открыли учебник на с.34. Что мы видим в рамке?
Д: То, что мы делали. Там же есть образец.
У: Попробуем решить пример у доски: 5 268: 2 174. Кто хочет объяснить? Остальные - слушают. Задаем вопросы, помогаем. Пользуемся образцом.
У: Как можно проверить решение примера на деление с остатком?
а: в = с (ост.d)
Кто запишет формулу?
Как проверить решение нашего примера?
Д: (учитель пишет на доске) 2 174 • 2 = 4 348
4 348 + 920 = 5 268
У: Читаем задание № 3.
Частных много. Выбираем любой пример из любого столбика верхней строчки. Из каких примеров будем выбирать?
Они одинаковы по сложности? Какой самый простой? А самый сложный? Выберите по силам.
Проверка: Самопроверка с доски. Образец: _ 947 I 312 900: 300 = 3
936 I 3
Проверка: 11 < 312, значит 
(остаток)
х312 +936
__ 311
936 947
У: У кого есть ошибки – подумайте, в чем причина. Отметьте красной пастой. Затем решите без ошибок.
У: У кого нет ошибок – устно № 10(а). В тетради – только ответ (красной пастой), не забудьте отметить номер.
*ФИЗМИНУТКА
У: Читаем задачу № 8.
После чтения задачи выберите нужную схему к задаче.
№ 1 № 2 № 3
в с? в с? в с а
А а?
У: Кто выбрал схему? Кто готов объяснить?
Д: 1 ученик – у доски.
У: Дома, для желающих (красная ручка): можете составить выражение и найти его значение.
*ФИЗМИНУТКА
У: Читаем задачи из № 9. Сначала под пунктом (А).
Читая, представьте себе, о чем говорится в задаче.
Читаем задачу № 9 (Б). Не просто читайте задачу, а попытайтесь представить себя на месте Толи.
У: А теперь ответьте на вопрос: Чем похожи задачи? Чем отличаются?
Как вы думаете, у них будет одинаковое решение? А ответ?
У: Посмотрите на доску. У меня записан алгоритм решения задачи:
1) 126 + 84 = J
2) J: 5 = J
3).....
4).....
У: Кто запишет 3-е и 4-ое действия?
Самостоятельно запишите задачу в тетрадь.
Кто хочет – придумайте задачу с другими величинами, имеющую такое же решение. Кто испытывает затруднение, поднимите красную карточку. Консультантами сегодня будут «Саша» и «Ира».
У: Послушаем задачи, которые вы придумали.
Итог урока
У: Чему мы сегодня научились?
Какой шаг в делении сделали?
Кому было трудно? В чем?
Кто может похвалить себя? За что?
Домашнее задание: Из № 2 и № 3 выбрать для себя 3 примера.
№ 8 – по желанию.
№ 6.
№ 7* или № 5 – по желанию.
Цель: вывести алгоритм деления на многозначное число (однозначное частное, деление с остатком).
Задачи:
1) актуализировать ЗУНы по делению на многозначное число (без остатка);
2) вывести алгоритм деления с остатком: нахождение цифры частного, запись;
3) вывести проверку частного;
4) развивать способность моделировать задачи; анализировать текст задачи.
Литература
1. Программа по математике. Объяснительная записка к программе.
2. Учебно-методические комплекты по программе: учебники, методические рекомендации.
3. Статьи из журналов:
1) А.А. Леонтьев. Что такое «деятельностный подход в образовании»// Начальная школа. Плюс-минус. № 1, 2001 г., с. 3-7.
2) В.Н. Рудницкая, Г.В. Юдачева. Математика, 1 класс (2 класс). Методика для учителя. Вектана-Граф. 2001 г.
3) Л.Г. Петерсон. Деятельностный подход и его реализация на уроках математики// Начальная школа. Плюс-минус. № 5, 1999 г., с. 24-31.
4) Е.Л. Мельникова. Проблемный урок в начальной школе или как открывать знания вместе с детьми// Начальная школа. Плюс-минус. № 5, 1999 г., с. 31-38.
5) И.И. Аргинская. Математика, 1 класс. Пособие к учебнику для 4-хлетней начальной школы. М., 2003 г.. с. 3-25, с. 46-48.
6) Виноградова Н.Ф. Начальная школа XXI века. Концептуальные основы построения учебно-методического комплекта для первого звена школы// Завуч начальной школы, № 1, 2002 г., с. 5-12.
7) Демидова Т.Е., Козлова С.А., Тонких Д.П. О новых учебниках для 1-4 классов «Моя математика»// Начальная школа, 2005 г.. № 8.
8) Н.Б. Истомина. Методика обучения математике в начальных классах. М.. 1997 г.. с. 243-249, с. 249-260.
9) И.И. Аргинская. Математика в системе общего развития// Начальная школа. Плюс-минус. № 4, 2000 г.
10) Т.Е. Демидова и др. «Моя математика» - новые учебники…// Начальная школа. До и после. № 4, 2005 г., с. 61-63.
11) Т.Е. Демидова и др. Моя математика. Методические рекомендации для учителя (1, 2, 3, 4).
12) Образовательная система «Школа 2100». Сборник программ.
13) Обучаем по системе Занкова Л.В. М., Просвещение, 1991 г., с. 5-18.
14) Е.Л. Мельникова. Проблемный урок…// Начальная школа. Плюс-минус. № 8, 1999 г., с. 41-45.
15) Нечаева Н.В. Занковский урок. Какой он?// Практика образования. 2004 г., № 4.
16) А.В. Белошистая. Методика обучения математике в начальной школе. Курс лекций. М., Владос, 2005 г., с. 358-401.
17) И.Я. Петрова. Проблемы…// Начальная школа. Плюс-минус. № 8, 1999 г. (3 программы).
18) Методические материалы к теме.
Замечания:
1. Из списка литературы необходимо выбрать только те статьи, которые имеют отношение к вашей программе обучения и конспекту урока.
2. Желательно самостоятельно подобрать дополнительные статьи (с 2000 г.) по анализируемой вами программе.
3. Список источников указать в контрольной работе.
Вопросы к зачету №1.
На зачете проверяются следующие методические умения студентов:
1) умение выделять порядок изучения темы, опираясь на учебники математики для детей.
2) умение конструировать фрагменты уроков по введению новых математических понятий ил способов действий: а) по теме «Нумерация», б) по теме «Арифметические задачи».
3) умение подбирать задания для диагностики сформированности ЗУНов на основе выделенных показателей.
I блок вопросов и заданий.
1) Перспективный план изучения одной из тем подготовительного периода. Его отражение в разных программах обучения детей математике (на выбор две программы).
2) Конспект урока по знакомству с числом (I концентр) – традиционная программа.
3) Конспект фрагмента урока по изучению нумерации чисел по любой из программ (кроме традиционной программы).
II блок вопросов и заданий.
1) Порядок изучения нумерации чисел I концентра (2 программы).
2) Порядок изучения нумерации чисел II концентра (2 программы).
3) Порядок изучения нумерации чисел III концентра (2 программы).
4) Порядок изучения нумерации чисел IV концентра (2 программы).
III блок вопросов и заданий.
1) Порядок изучения КС сложения и вычитания (2 программы).
2) Порядок изучения КС умножения и деления (2 программы).
3) Порядок изучения сложения и вычитания в I концентре (2 программы).
4) Порядок изучения сложения и вычитания в пределах 20 (2 программы).
5) Порядок изучения внетабличного сложения и вычитания (2 программы).
6) Порядок изучения таблиц умножения и деления (2 программы) с теоретическими основами.
7) Порядок изучения внетабличного умножения и деления (2 программы) с теоретическими основами.
IV блок вопросов и заданий.
Полная методика (подготовка, введение, закрепление) для приема вида (традиционная программа).
1) 42 – 7;
2) а + 3 (I концентр);
3) 36 + 20;
4) 72: 4;
5) 72: 24;
6) 12 – 7 (один из приемов);
7) а + 5, 6, 7, 8, 9;
8) алгоритм письменного умножения на двузначное число;
9) алгоритм письменного деления на двузначное неразрядное число.
V блок вопросов и заданий.
1) Задания для изучения сформированности ЗУНов по теме «Нумерация чисел I концентра».
2) Задания для изучения сформированности ЗУНов по теме «Нумерация чисел II концентра».
3) Задания для изучения сформированности ЗУНов по теме «Нумерация чисел III концентра».
4) Задания для изучения сформированности ЗУНов по теме «Нумерация чисел IV концентра».
5) Задания для изучения сформированности навыков сложения и вычитания в пределах 10.
6) Задания для изучения сформированности навыков внетабличного сложения и вычитания в пределах 100.
7) Задания для изучения сформированности навыков письменного умножения на однозначное число.
На зачете студент получает задания из каждого блока (по одному заданию). В случае подготовки студентом по одному из блоков заданий на п/з преподаватель может уменьшить количество сдаваемых блоков.
Вопросы к зачету № 2.
I. Опишите этапы работы по решению задачи в соответствии с планом
1) типовая задача (какая) или нетиповая;
2) все возможные виды моделей к данной задаче;
3) поиск решения «от вопроса» (в вопросно-ответной форме). Схема поиска решения;
4) поиск решения «от данных» (в вопросно-ответной форме). Схема поиска решения;
5) план решения (в вопросно-ответной форме);
6) запись решения (по действиям с письменным пояснением). Запись ответа.
7) все возможные виды проверки решения данной задачи;
8) два варианта работы над решенной задачей (кроме проверки).
II. Предложите фрагмент урока по введению задачи нового вида
1) на нахождение неизвестного уменьшаемого;
2) на разностное сравнение;
3) типовая задача на движение (одновременное движение двух тел в случае их сближения (или удаления));
4) задача на пропорциональное деление.
III. Предложите не менее трех приемов работы над задачей, направленных на формирование общих умений решать задачи (см. задачу из п. № I).
Контрольная работа № 2.
Цель:
· формирование умений составлять конспекты уроков с учетом принятой в системе обучения технологии и с учетом современных требований к уроку математики;
· формирование умений реализовывать положения проблемно-диалогового обучения при составлении фрагментов уроков математики;
· формирование умений использовать задачи из учебника в соответствии с определенными целевыми установками.
· формирование умений проводить диагностику сформированности ЗУНов по математике.
Содержание.
Задание № 1.
I. Составьте конспект фрагмента урока с учетом принятой в данной программе технологии урока, целевых установок программы:
1) введение к.с. деления (деление на равные части) по программе Демидовой и др.
2) введение таблицы умножения и деления с числом 2 (программа Рудницкой В.Н.).
3) введение величины «масса», сравнение массы непосредственным путем (программа Аргинской И.И.)
4) введение понятия «класс» (программа Аргинская И.И.).
5) введение понятия «задача» (по программе Петерсон Л.Г. или Демидова и др.).
6) введение одного из уроков по теме деление с остатком (по программе Аргинской И.И.).
7) введение понятия «выражение с переменной» («Школа России»).
8) введение любого алгоритма письменного деления (или его части) (программа Аргинской И.и.).
9) введение чисел 1-10 (любого числа или группы чисел) (программа Рудницкой В.Н. или «Планета Знаний»).
10) введение окружности или круга (по любой из программ, программу указать).
Задание № 2.
Выполните анализ предложенного фрагмента урока математики с позиции реализации основных положений проблемно-диалогового обучения.
Фрагмент № 1.
Цель: ввести способ решения примера 40 – 6.
У: сейчас я предложу каждому из вас найти значение выражения на карточке. В случае, если вы не можете решить пример, …? (84 – 27 =?) если можете решить, но есть сомнение, то решите, но рядом тоже поставьте знак?.
48 – 3 =
56 – 4 =
70 – 8 =
39 – 8 =
60 – 7 =
78 – 6 =
80 – 3 =
У: Стоп.
Руки вверх, вперед, вверх.
У: в группах (2 парты) обсудите ваши решения. На отдельном листе выпишите выражения, в которых затрудняется большинство членов группы. Попробуйте ответить, чем эти выражения отличаются от тех, которые вы не выделили. Попробуйте выделить, в чем причина затруднений. Попробуйте выделить тему урока. Время: 3 минуты.
У: Выслушайте мнение группы (2 группы, по «считалке»).
У: дети (по одному от группы) высказывают позицию группы. Если нет нового – то соглашаются с предыдущей группой.
У: Обобщает сведения группы. предлагает кому-то из класса сформировать тему урока: Вычитание из круглого числа однозначного.
У: рассмотрим одно из выражений: 60 – 7. Какие есть предложения по способу решения этого примера? (Дети предлагают). Один из примеров: 60 = 50 + 10, 10 – 7 = 3, 50 + 3 = 53.
У: Можно ли этот способ пояснить на предметной модели.
Один у доски показывает решение с тетради.
У: Что произошло в ответе числа с десятком? (Уменьшилось на 1 десяток).
У: Кто может сформулировать способ решения любого из таких примеров (по шагам).
Фрагмент № 2.
Цель: ввести понятие «выражение», выделить существенные признаки этого понятия.
У: На доске у меня математические записи. Разбейте их на 3 группы:
14 – 3 8 + 5 7 + 3 = 11 12 – 8 = 4 8 – (3 + 2)
6 > 4 8 < 16 15 + 3 – 1
Д – индивидуально разбивают по группам, пишут ответы на листочке. (2 минуты).
У: Обменяйтесь листочками в четверке. Если придете к общему мнению. Запишите его на листочке. Если будут разные мнения (обоснованные), то запишите их (3 минуты).
У: Представители групп объясняют, найдите общие, выпишите на доску (3 минуты).
У: В это время мы с вами вспомним названия компонентов в действиях. первое слагаемое 8, второе слагаемое 4, найти сумму. Вычитаемое 6, разность 2. Когда сумма равна слагаемому? Может ли разность равняться вычитаемому?
Проверка работы групп.
После анализа работы групп останавливаются на варианте:
14 – 3 6 > 4 7 + 3 = 11
8 + 5 8 < 16 12 – 8 = 4
15 + 3 – 1
8 – (3 + 2)
У: Название каких записей вы знаете?
Д:
| 6 > 4 |  это неравенства
| 7 + 3 = 11 |  это равенства
|  14 – 3
| это примеры |
| 8 < 16 | 12 – 8 = 4 | 8 + 5 | |||
| 15 + 3 – 1 | |||||
| 8 – (3 + 2) |
У: В математике для записей данного вида используют другой термин. Может кто-то уже знает? Попробуйте разгадать:
| в | р | н | е |
У: Попробуйте объяснить, какая запись называется «выражение»? Что в ней может быть? Составьте выражение.
Фрагмент № 3.
Цель: введение единой мерки для измерения длины.
У: Вызывает к доске двух учеников, предлагает им измерить с помощью мерок длину отрезка (мерки и отрезки другие дети не видят). Пока измеряют длину, учитель (У) задает вопросы классу.
1) у каких линий, изображенных на доске можно измерить длину?
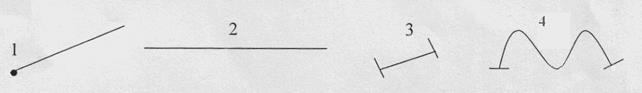
Д: у фигур № 3 и № 4.
2) У: Сравните длины отрезков.
У: Рассмотрим работу учеников у доски. Как вы поняли задание? Какая получилась длина?
1 ученик: 3 мерки.
2 ученик: 5 мерок.
У: Какой вывод можно сделать о длине отрезков, которые измерили ученики?
Д: У второго длина больше, чем у первого.
У: Проверим: дети видят отрезки (на переносных досках), причем видно, что первый отрезок длиннее второго.
№ 1 № 2
У: Не понимаю. Вы сказали, что второй длиннее, у него 5 мерок, а первый короче – у него 3 мерки. А мы видим, что наоборот. В чем причина?
Задание № 3.
1) Выполните анализ заданий из учебника математики:
а) по содержанию;
б) по дидактической цели (этапы в изучении учебного материала);
в) по характеру познавательной деятельности учеников.
2) Определите цель урока (фрагмент урока – если программа Аргинской И.И.), образовательные задачи урока.
3) Ответьте на вопрос: есть ли специальные задания на формирование контрольно-оценочной деятельности? (Если есть – объясните). Предложите свои варианты.
4) Как бы вы провели итог урока? Рефлексию?
Задание № 4.
Выполните анализ фрагмента урока по программе Аргинской И.И. с позиции реализации основных дидактических принципов обучения Л.В. Занкова. Для этого:
а) Выполните анализ заданий учебника (Аргинская И.И. Математика, 1 класс, учебник, Самара, 2003 г.).
б) Сформулируйте задачи фрагмента урока.
в) Затем сформулируйте каждый принцип, раскройте его содержание и выполните анализ (каждый принцип рассматривается отдельно).
Фрагмент № 1.
№ 178 (1 класс)
У: Рассмотрите пары чисел (запись на доске):
4 3 6 7 5 8 7 2
Какое задание с ними вы можете предложить? (выполнить сложение, сравнить числа…).
У: Сравните числа и поставьте знак сравнения (фронтальная работа, один ученик у доски ставит знак, остальные, по его просьбе, говорят, какие знаки надо ставить и читает название).
У: Как называются эти записи? почему?
У: А теперь я хочу предложить интересное и новое задание с этими неравенствами. Кто может высказать предложение, какое новое задание можно предложить? (разбить на группы – У – это было…).
У: Превратить каждое неравенство в равенство. есть вопросы? (Хорошо, если спросят, что значит «превратить». У – Кто понял? Превратить – изменить одну из частей так, чтобы получилось равенство, т.к. задание новое, работаем в группах (постоянные группы)).
Для начала каждая группа рассмотрит неравенство 4 > 3.
Проверка:
Свои выводы группа пишет на доске. Представитель объясняет как получили каждое равенство. Итог: 3 = 3, 4 = 4, 4 = 3 + 1 (Если кто-то 4 – 1 = 3 – это новое для учеников, но возможное).
У: Теперь каждый самостоятельно выберите любое неравенство и превратите его в равенство.
Проверка:
У: Кто рассмотрел пару чисел 5 и 8. Назовите равенства. Кто рассмотрел пару чисел 6 и 7. Назовите равенства. Кто рассмотрел пару чисел 7 и 2. Назовите равенства.
У: Объясните как вы нашли число 3 в равенстве 5 + [] = 8. как нашли число 5 в равенстве 7 = 2 + []? Почему в 3 равенстве везде стоит знак сложения?
У: Кто теперь может объяснить, как неравенство обратить в равенство?
У: Как бы вы озаглавили эту часть урока?
Физминутка.
Фрагмент № 2.
У: Читаем задание № 179 (1 класс). Что необходимо для выполнения этого задания?
У: Скользко отрезков начертим? (Обсуждение).
(Учитель при объяснении детям использует числовой луч).
Итог: 3 отрезка длиной 4, 5, 6 см.
У: Выполняем задание.
У: Кто объяснит, какую ошибку можно допустить при черчении отрезков?
У: Читаем II задание.
У: Какие буквы мы уже использовали в похожих заданиях (А, Е, М, К, О). Хватит ли этих букв? используйте эти буквы. Добавьте свою букву.
У: Читаем III задание. Кому непонятно? Выполняем.
Проверка:
У: В соседнем классе выполняли это задание. У них получились такие неравенства.
Карточка 1
У: Догадайтесь, какими буквами обозначали каждый отрезок. Докажите.
У: Все ли возможные неравенства они составили?
У: Рассмотри свои неравенства. У тебя их столько же? Если нет, то дополни. Подумайте, что помешало тебе записать все неравенства. Как бы вы озаглавили III часть урока?
Итог: Что оказалось новым для вас на уроке? Что вызвало интерес? Где было трудно? Работу кого на уроке вы бы хотели отметить особо? Какие достижения у себя вы бы выделили? Какие проблемы?
Домашнее задание: № 180.
Фрагмент № 3 (№ 344, 3 класс).
У: Прочитайте выражение разными способами
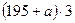
Д – читают – фронтальный опрос.
У: Какие значения может принимать переменная 
в этом выражении?
Д: Любые, начиная с нуля.
У: Найдите значения выражения (в тетради) при 
, 
, 
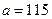. Если сомневаетесь в ответе, ставьте рядом знак?.
Проверка: Какие значения отметили? Почему? (Если нет, то фронтальный опрос – способ решения и ответ).
У: Чем похожи значения выражений?
Д: Они – трехзначные числа.
У: 1) При каком наименьшем значении выражение будет трехзначным числом?
2) При каком наибольшем значении сохранится трехзначный результат (оба вопроса записаны на доске).
Отвечаем на каждый отдельно. Работаем в группе (группа постоянного состава).
Результаты работы и как к нему пришли группа оформляет на доске. Время 4 минуты (3 минуты на обсуждение, 1 минута – на оформление).
Проверка. Сообщение групп. Обсуждение.
У: Работаем самостоятельно. Выполняем задание № 3 из № 344. Предыдущее задание можете использовать.
Проверка: взаимная проверка в парах.
У: Как использовали предыдущее задание? Оцените работу товарища.
У: Как озаглавим эту часть урока? Какие возникли трудности? Чью работу вы бы выделили?
Фрагмент № 4 (№ 333, III класс).
У: Ребята посмотрите на доску. Что вы видите?
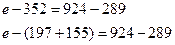
Д: Уравнения.
У: По каким признакам сделали вывод?
Д: Есть неизвестное число, есть равенство.
У: Чем похожи и чем отличаются уравнения?
Д: …
У: Найдите среди них более сложное. Сколько надо выполнить действий, чтобы решить выбранное уравнение? Объясните.
Д: 2, 3, 4. Объясняют.
У: Открыли тетради. Решаем уравнения, проверяем предположения.
Работаем по четверкам (постоянные группы). Решение должно быть у каждого в тетради. Если возникли вопросы, сформулируйте их. Попробуйте сформулировать алгоритм решения похожих уравнений.
Дети работают в четверках.
Проверка. Представитель одной группы записывает решение на доске. В это время дети формулируют вопросы, алгоритм.
Самопроверка с доски. Вопросы детей представителю группы и группе.
Вывод общего алгоритма.
У: Будет ли найденное число корнем другого уравнения?
Д: …
У: проверьте свое предположение. Запишите уравнение и значение 
в тетради, сделайте проверку. 1 ученик – у доски.
Проверка: самопроверка с доски.
Оценочные суждения по работе ученика у доски.
У: Решите уравнение (самостоятельно в тетради. № 333, задание 5, стр. 148). Выберите одно уравнение (любое). Время – 3 минуты. До решения выполните самооценку своих умений решать подобные уравнения.
Используются кружки:
 |
Проверка: самопроверка с доски (2 человека решали на доске).
После проверки – итоговый знак самооценки. Обсуждение оценочной деятельности.
У: Составьте свое уравнение такой же трудности (время – 1 минута), решать не надо.
Дети составляют.
Проверка: обсуждение. Возникновение проблемы: не все уравнения можно решить в целых числах.
У: какое условие не все учащиеся выделили? (чтобы уравнение решалось в целых неотрицательных числах)
У: дома составьте и решите похожие уравнения с соблюдением этого условия.
У: сформулируйте тему части нашего урока.
Фрагмент № 5 (№ 177, I класс).
Ход урока.
У: Открыли тетради. Запишем число, классная работа. Достаньте конверты с кружками.
У: Положите слева 5 кругов, а справа 4 круга. Объедините все кружки. Запишите действие, которые вы выполнили и его результат в тетради.
Проверка. Один ученик читает равенство, дети задают вопросы.
У: Положите на парту 9 кругов. Уберите 3 круга. Попробуйте изобразить это действие в тетради с помощью рисунка.
Проверка: Учитель вызывает к доске учеников, рисунки которых вызывают интерес с точки зрения анализа.
(ΟΟΟΟΟΟΟΟΟ) (ΟΟΟΟΟΟnnn) (OOOOOOOOO)
¯ ¯ ¯
(OOOOOOÆÆÆ) (OOOOOOOOO)
Выясняют, какие рисунки передают смысл действия. Учитель выделяет те, которыми обычно пользуются в математике.
(OOOOOOÆÆÆ) (OOOOOOOOO)
У Сравните рисунки с моим. В чем сходство?
| OÆOOOÆOÆO В чем разница? |
Возможно ли? Важно ли, какие круги зачеркнули? Когда?
У: Похоже ли действие, которое мы сейчас выполнили на первое действие с кружками? Какой вывод вы можете сделать? (Это другое действие, не сложение. Его надо назвать).
У: Может кот-то уже знает, как называется действие, когда убирают часть предметов? (Если нет ответа – учитель сам называет).
На доске: Когда убирают часть предметов, выполняют действие вычитания.
У: Составьте рассказ, в котором надо выполнить действие вычитания. Предметы выберите сами.
Проверка: несколько детей предлагают рассказы, остальные сигнализируют «правильно», «неправильно».
У: Чей рассказ вы бы выделили? Почему?
У: Как бы вы озаглавили эту часть урока?
Физминутка.
