Аналіз впливу режимів споживання електроенергії групи споживачів на електроспоживання України

 

Для аналізу впливу графіка навантаження споживача (ГНС) на графік навантаження енергосистеми (ГНЕС) були розроблені інтегральні різноманітні коефіцієнти, суть яких зводиться до можливості як обліку ваги даної групи споживачів, так і направленість коливань потужності.

З точки зору маркетингу, основна задача зводиться до виявлення цільової групи, з якою необхідно буде працювати при формуванні, як тарифної політики, так і різного роду комунікацій.

Розрахунок коефіцієнта внеску: 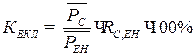(8.5),

де 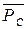– середнє значення навантаження споживача; – середнє значення навантаження енергосистеми; 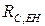- коефіцієнт кореляції, який розраховується по формулі:

(8.6)

Мета коефіцієнту впливу – врахувати при аналізі графіка навантаження, як міру впливу споживача, так і його регулювальні здібності. Перевагою даного коефіцієнту є збалансованість кінцевого результату, тобто сума отриманих коефіцієнтів дорівнює 100%.

Розрахунок коефіцієнта впливу:

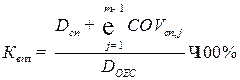(8.7),

де 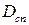, 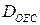_i –дисперсія добових графіків навантаження досліджуваного споживача та ОЕС України відповідно, 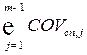– сума коваріацій між досліджуваним та добовими графіками споживачів, m – загальна кількість графіків, що складають сумарне навантаження енергосистеми.

Розрахуємо вказані вище коефіцієнти. Отримані значення зведемо у таблицю.

Для аналізу графіків навантаження і співставлення їх з графіками інших споживачів використовуються групові коефіцієнти. Розрахуємо групові коефіцієнти за 2 режимних дні 2012-2013 років:

Розрахуємо даний коефіцієнт, згідно методики, для 2012-2013 років та занесемо отримані результати до таблиці 7.3:

 

Таблиця 8.3 – Групові коефіцієнти

 

Показник	Період
20.06.12	19.12.12	19.06.13	18.12.13
R	0,73524	0,68459	0,66016	0,63185
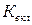
	0,314	0,324	0,289	0,275
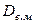
	601,1			915,4
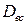
			1387,53	1848,57
		46755,4
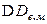
	27735,1	47908,4		38779,4
		48920,4	23608,53	39712,57
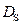
	57183,1	96828,8	46396,53	78491,97
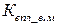
	1,224	1,18	1,05	0,98
	1,29	1,209	1,09	1,01

 

 

За результатами проведених розрахунків можемо зробити висновок, що графік навантаження групи має значну нерівномірність, вищу за нерівномірність графіка ОЕС України (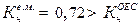) досить виражене пікове навантаження ()

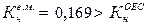та більшою мірою заповнює ранковий максимум енергосистеми. Разом з тим, група не має істотного впливу на графік ОЕС України, що зумовлено невеликим загальним обсягом її електроспоживання.

Зміну даних коефіцієнтів 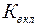та 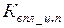по роках приведемо на рис. 8.9.

 

 

Як свідчить графік, приведений на рисунку, протягом розглянутих років коефіцієнти змінювались в незначних межах, причому коефіцієнти впливу приймають дещо більші значення влітку, ніж взимку (виключення – зимовий режимний день 2008 року), а коефіцієнти вкладу приймають дещо більші значення взимку, ніж влітку. Це свідчить про наявність температурної залежності попиту на електричну енергію.

 

8.3 Формування груп споживачів за ступенем впливу на режим споживання електроенергії в Україні(кластерний аналіз)

 

Кластерний аналіз проводиться для формування груп споживачів. Для цього розглянемо 6 основих груп споживачів електроенергії. Проведемо розподіл на групи по шести критеріям: 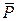(середня потужність, МВт), (дисперсія графіку навантаження), (коефіцієнт навантаження), 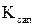(коефіціент заповнення графіку), 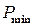(мінімальне навантаження, МВт), 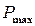(максимальне навантаження, МВт).

Приведемо приклад розрахунку кластерного аналізу для зимового режимного дня 2013 року. Зведемо в таблиці 8.4 вихідні дані, розрахуємо середнє значення, середньо квадратичне відхилення для кожного критерія:

 

Таблиця 8.4 – Параметри для проведення кластерного аналізу

Групи споживачів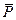
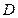
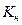
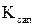
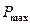
I. Промисловість в цілому			0,761	0,884
II. Електротехнічне машинобудування			0,359	0,593
III. Транспорт			0,738	0,859
IV. Будівництво		737,38	0,502	0,728
V. Комунальне господарство		7078,2	0,789	0,901
VI. Інші пром. підпр.		1848,6	0,706	0,87
Середнє	1807,5	49971,1	0,642	0,805		1988,8
Середньо квадратичне відхилення	3176,194	73759,35	0,172493	0,121216	2966,514	3419,076

 

Проведемо нормалізацію даних, що дасть змогу при розбитті на групи, врахувати кожний критерій у рівній мірі. Нормалізацію кожного критерія проведемо за наступною формулою:

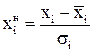(8.9)

де 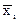– середнє значення параметра; – середньоквадратичне відхилення.

Отримані нормалізовані значення параметрів зводимо у таблицю 8.5.

 

 

Таблиця 8.5 – Нормалізовані параметри для проведення кластерного аналізу

Групи споживачів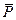
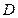
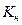
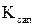
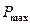
I. Промисловість в цілому	2,024593	1,44871	0,689883	0,651729	2,024936	2,02429
II. Електротехнічне машинобудування	-0,54263	-0,66508	-1,64065	-1,74894	-0,53969	-0,54015
III. Транспорт	-0,24416	1,117823	0,556544	0,445486	-0,24945	-0,24855
IV. Будівництво	-0,53444	-0,66749	-0,81163	-0,63523	-0,53126	-0,53751
V. Комунальне господарство	-0,26809	-0,58152	0,852208	0,791975	-0,26361	-0,25908
VI. Інші	-0,43527	-0,65243	0,37103	0,536233	-0,44092	-0,43895

 

Визначимо міру подібності між даними групами, шляхом знаходження Евклідової відстані між парами груп за наступною формулою:

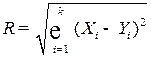(8.10)

Наведемо приклад розрахунку Евклідової відстані між промисловістю в цілому та сільгоспспоживачами:

Бачимо, що Евклідова відстань достатньо велика, тому можна стверджувати, що ці групи споживачів дуже відрізняються за обраними параметрами.

На основі результатів розрахунків будується матриця відстаней та зведиться у таблицю 8.6:

 

Таблиця 8.6 – Матриця відстаней №1

	I	II	III	IV	V	VI
I		5,95	3,957	5,295	4,458	4,767
II			3,617	1,388	3,593	3,05
III				2,544	1,76	1,803
IV					2,243	1,673
V						0,627
VI

 

Мінімальна відстань – між комунальним господарством (V) та іншими галузями (VI). Їх об’єднуємо в одну групу –V+VI. Відстані між даною групою та рештою галузей визначимо за допомогою формули «найближчого сусіда»:

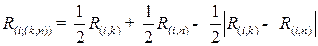(8.10)

 

Провівши розрахунки, будуємо нову матрицю відстаней:

 

Таблиця 8.7 – Матриця відстаней №2

	I	II	III	IV	V+VI
I		5,95	3,957	5,295	4,458
II			3,617	1,388	3,05
III				2,544	1,76
IV					1,673
V+VI

 

Мінімальна відстань – між сільгоспоживачами (II) та отриманою вище групою (III+V). Їх об’єднуємо в одну групу – ІІ+III+V.

Надалі розрахунки повторюються.

 

Таблиця 8.8 – Матриця відстаней №3

	I	ІІ+IV	III	V+VI
I	0,000	5,295	3,957	4,458
ІІ+ IV		0,000	3,617	3,05
III			0,000	1,76
V+ VI				0,000

 

Мінімальна відстань – між будівництвом (IV) та отриманою вище групою (ІІ+III+V). Їх об’єднуємо в одну групу – ІІ+III+IV+V.

Зведемо нову матрицю відстаней:

 

Таблиця 8.8 – Матриця відстаней №3

	I	ІІ +IV	III+ V+VI
I	0,000	5,295	3,957
ІІ +IV		0,000	3,05
III+ V+VI			0,000

 

 

Мінімальна відстань – між промисловістю (I) та отриманою вище групою (ІІ+III+ IV+V). Їх об’єднуємо в одну групу – І+ІІ+III+IV+V.

Зведемо кінцеву матрицю відстаней:

 

Таблиця 8.9 – Матриця відстаней №4

	І	ІІ +IV+ III+ V+VI
І	0,000	3,957
ІІ +IV+ III+ V+VI		0,000

За результатами кластерного аналізу будуємо дендограму (рис. 8.9), яка показує послідовність обєднання споживачів у групи і дає можливість на певних етапах вибрати необхідну кількість груп

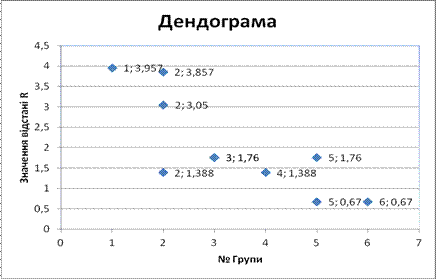
Рисунок 8.9 – Дендрограма об’єднання груп споживачів за кластерним аналізом для зимового режимного дня 2013 року