Используя элементарные преобразования строк, матрицу приводят к трапециевидной или треугольной форме, далее ранг находят по определению.
Как частный случай последнего метода, может быть рассмотрен метод нулей и единиц: элементарным преобразованием строк матрицу приводят к эквивалентной, состоящей или из нулевых строк и столбцов, или из строк и столбцов, в которых содержится ровно одна единица, а остальные элементы – нулевые. Количество единиц в такой матрице равно ее рангу.
Пример 1. Исследовать матрицу A на невырожденность, найти А –1, если она существует, результат проверить.
Решение. Вычислим определитель матрицы A
Невырожденность матрицы A означает, что существует единственная обратная ей матрица А –1.
1-й способ. Используя формулу (13.4), найдем алгебраические дополнения:
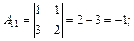
Тогда 
и по формуле (13.4) имеем:
(13.5)
2-й способ. Воспользуемся эквивалентностью матриц 
и 
Следовательно, 
Для контроля правильности результата достаточно проверить условия 
Действительно,
Аналогично 
Пример 2. Решить матричное уравнение
Решение. Запишем уравнение в виде
(13.6)
где A, B, C – заданные матрицы.
Умножим уравнение (13.6) слева на А –1 и справа на В –1. Тогда справедливо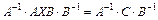 
или, учитывая определение обратной матрицы, 
Найдем А –1 и В –1:
Тогда
Значит, 
Пример 3. Доказать, что матрица A является ортогональной, т. е. для нее выполняется равенство 
Решение. Найдем АТ и проверим равенство 
Мы доказали ортогональность матрицы A.
Пример 4. Найти ранг матрицы
Решение. 1-й способ. Воспользуемся методом окаймляющих миноров. Фиксируем 
Для М 2 окаймляющими будут два минора 3-го порядка:
Значит, rA = 2, а базисным минором можно считать, например, М 2.
2-й способ. Преобразуем матрицу A:
Ранг последней матрицы равен двум, следовательно, таков же ранг исходной матрицы.
З а м е ч а н и е. О том, что ранг матрицы A равен 2, можно было судить на третьем шаге преобразований (во 2-м способе), когда получили нулевую строку и ненулевой минор (выделен) максимального порядка 2.
Задания
I уровень
1.1. Найдите обратные матрицы для следующих матриц:
1) 
2) 
3) 
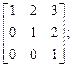4) 
1.2. Решите матричное уравнение:
1) 
2) 
3) 
4) 
1.3. Найдите какой-либо базисный минор матрицы:
1) 
2) 
3) 
1.4. Определите ранг матрицы:
1) 
2) 
II уровень
2.1. Найдите обратную матрицу для заданной матрицы, используя формулу (13.4):
1) 
2) 
3) 
4) 
2.2. Методом эквивалентных преобразований найдите обратные для следующих матриц:
1) 
2) 
3) 
2.3. Решите матричное уравнение (найдите матрицу X):
1) 
2) 
3) 
4) 
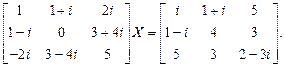
2.4. Найдите ранг матрицы:
1) 
2) 
3) 
4) 
III уровень
3.1. Найдите ранг матрицы в зависимости от значения параметра а:
1) 
2) 
3.2. Определите, какие из приведенных матриц удовлетворяют соотношению 
где 
– матрица, элементы которой являются комплексно-сопряженными с элементами матрицы A:
1) 
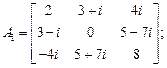2) 
3) 
4) 
3.3. Найдите обратные матрицы для следующих матриц:
1) 
2) 
