1) 
2) 
3) 
4) 
Если для квадратной матрицы A выполняется соотношение  то матрица A называется симметрической матрицей, а если
то матрица A называется симметрической матрицей, а если  – то кососимметрической.
– то кососимметрической.
Элементарными преобразованиями над строками матрицы A называют следующие операции:
1) перестановку строк;
2) умножение строки на ненулевое число;
3) прибавление к элементам строки соответствующих элементов другой строки, умноженных на ненулевое число.
Говорят, что матрица A эквивалентна матрице B (пишут: A~B), если матрица B получена из A при помощи элементарных преобразований строк.
Пример 1. Найти 2 A – 3 B, если

Решение. Прежде всего следует заметить, что матрицы A и B имеют одинаковый размер 2×3. Поэтому по определению линейных операций над матрицами имеем:

Пример 2. Если возможно, вычислить соответствующие произведения и проверить справедливость равенства AB = BA для следующих пар матриц:
1)  2)
2) 
3)  4)
4) 
5) 
Решение. 1) Матрицы A и B согласованные, так как матрица A имеет размер 2×2, а матрица B – размер 2×3, т. е. количество столбцов матрицы А совпадает с числом строк матрицы B.

Умножение матрицы B на матрицу A невозможно, так как матрицы не согласованы (число 3 столбцов матрицы B не равно числу 2 строк матрицы A).
2) Произведения AB и BA могут быть найдены, так как в обоих случаях матрицы согласованы:

 .
.
Приходим к выводу, что 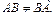
Приведенный пример иллюстрирует не только отсутствие свойства коммутативности операции умножения для многих согласованных для этого действия матриц, но и показывает, что при умножении двух ненулевых матриц может быть получена нулевая.
3) Матрицы A и B согласованы для умножения, но произведения AB и BA имеют разные размеры и элементы:


AB и BA – квадратные матрицы размеров 3×3 и 2×2 соответственно, 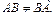
4) 

Приходим к заключению, что 
Очевидно, что условие будет соблюдаться для любых диагональных матриц одного размера.
5) Матрицы A и B согласованы для умножения:


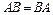 при соблюдении условий:
при соблюдении условий: 


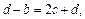 т. е. при
т. е. при 
 Таким образом, матрица A является коммутативной с матрицей
Таким образом, матрица A является коммутативной с матрицей  или
или 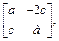 где a, b, с – любые действительные числа.
где a, b, с – любые действительные числа.
Пример 3. Найти матрицу X, удовлетворяющую условию  если известна матрица
если известна матрица 
Решение. Запишем равенство  в виде
в виде 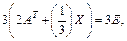 а затем
а затем  и, наконец,
и, наконец,  Поскольку
Поскольку  то
то
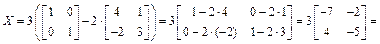

Пример 4. Найти значение матричного многочлена f (A), если 
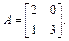
Решение. По условию задачи

Пример 5. Привести матрицу А к треугольному виду с помощью элементарных преобразований строк, если

Решение. Поменяв строки местами, получим матрицу, эквивалентную исходной:

Затем запишем вместо второй строки сумму первой, умноженной на (–2), и второй, а вместо третьей – результат сложения первой, умноженной на (–3), и третьей:

Осталось прибавить к третьей строке вторую, умноженную на (–2):

В результате получена треугольная матрица, эквивалентная матрице A.
Эти преобразования (без комментария) записывают в виде

Задания
I уровень
1.1. Найдите линейную комбинацию 3 A + 2 B матриц A и B, если:
1) 

2) 

3) 
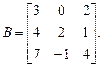
1.2. Вычислите:
1)  2)
2) 
3)  4)
4) 
1.3. Найдите значения f (A) и f (B) функций f (х), если:
1) 
2) 
1.4. Приведите матрицу к трапециевидной или треугольной форме:
1) 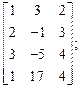 2)
2)  3)
3) 
1.5. Пусть  Найдите
Найдите 
II уровень
2.1. Найдите сумму, разность и произведение матриц A и B, если:
1) 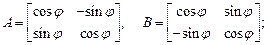
2) 
3) 
2.2. Выполните действия:
1) 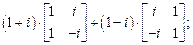
2) 
3) 
2.3. Вычислите n -ю степень матрицы, n Î N:
1)  2)
2) 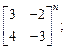 3)
3) 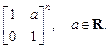
2.4. Найдите матрицу X из условия

2.5. Найдите 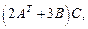 если:
если:
1) 
2) 
2.6. Найдите значение функции f(A), если:
1) 
2) 
III уровень
3.1. Возведите матрицу в степень:
1) 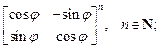 2)
2) 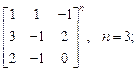
3) 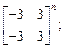 4)
4) 
3.2. Найдите матрицы, коммутативные (перестановочные) с заданной:
1)  2)
2)  3)
3) 
3.3. Найдите матрицы второго порядка, квадрат которых равен:
1) нулевой матрице; 2) единичной матрице.
3.4. Определите условие, при котором справедливо равенство:
1) 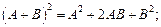 2)
2) 
3.5. Для матриц A и B докажите равенство:
1)  2) (A + B) T = AT + BT;
2) (A + B) T = AT + BT;
3) (kA) T = kAT, где k – число; 4) (AB) T = BTAT.






