Для машинной реализации операции умножения двоичных чисел необходимо иметь, как минимум, регистр множимого и регистр множителя, в которые перед началом операции записывают соответственно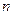 
-разрядные множимое 
и множитель 
, и сумматор, в котором образуется произведение 
, вычисляемое путем ряда сложений соответствующим образом сдвинутого относительно разрядной сетки множимого с предшествующей суммой частичных произведений.
Очевидно, что максимальное количество слагаемых (частичных произведений) равно 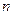. Процессом суммирования управляют цифры множителя. Если очередная цифра множителя единица, то к предшествующей сумме частичных произведений прибавляется множимое, взятое с соответствующим весом. Если очередная цифра множителя нуль, то суммирование не производится, а осуществляются необходимые сдвиги чисел в регистрах и сумматоре. Как указывалось выше, множитель можно анализировать последовательно, начиная как с младших, так и со старших разрядов.
Из сказанного следует, что возможно использовать несколько машинных технологий для реализации операций умножения чисел в прямом коде с фиксированной запятой. Для их рассмотрения обозначим произведение через 
, множимое через 
, а множитель 
представим в развернутом виде:
.
Тогда произведение можно записать следующим образом:
. (2.1)
Для удобства машинной реализации представим это выражение в циклическом виде. Таких форм представления обычно используют четыре, в соответствии с которыми чаще всего применяют следующие машинные технологии выполнения операции умножения чисел с фиксированной запятой.
Технология 1
Представим произведение в виде
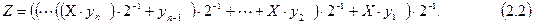
Из (2.2) следует, что в каждом из 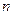циклов умножения вычисляется
, (2.3)
при этом в начале умножения индекс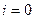 
и 
.
После выполнения 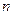циклов в сумматоре образуется 
, равное полному произведению: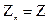 
.
Функциональная схема реализации рассматриваемой технологии представлена на рис. 2.1.
Рис. 2.1. Первая технология умножения
Каждый цикл умножения младшими разрядами вперед сводится к передаче в сумматор множимого X, умноженного на цифру множителя 
, т. е. к передаче в сумматор, если 
, к непередаче, если 
, и к умножению суммы на 
, т.е. сдвигу вправо на один разряд.
Умножение начинается с младших разрядов множителя, т.е. множитель сдвигается вправо. После каждого такта суммирования сумма частичных произведений сдвигается вправо. Множимое не сдвигается в регистре 
.
Технология 2
Представим произведение в следующем виде
. (2.4)
Из анализа (2.4) следует, что в каждом из 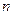циклов умножения вычисляется
, (2.5)
где 
, а в начале умножения
.
После выполнения 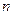циклов в сумматоре образуется 
.
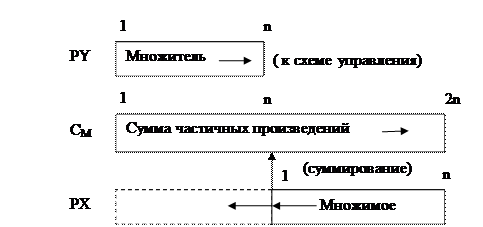Функциональная схема реализации рассматриваемой технологии умножения представлена на рис. 2.2.
Рис. 2.2. Вторая технология умножения
Таким образом, в данной технологии каждый цикл умножения сводится к сдвигу множимого влево на один разряд и к передаче его в сумматор, если , или не передаче, если .
Умножение начинается с младших разрядов множителя, т.е. множитель в каждом цикле сдвигается вправо. После каждого такта суммирования множимое сдвигается влево. Сумма частичных произведений неподвижна и накапливается в сумматоре СМ.
Технология 3
Представим произведение в виде
. (2.6)
|
Из анализа (2.6) следует, что
, (2.7)
причем в начале умножения 
После 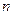циклов умножения в сумматоре сформируется 
.
Функциональная схема реализации данной технологии умножения представлена на рис. 2.3.
Рис. 2.3. Третья технология умножения
В данной технологии умножения каждый цикл сводится к передаче множимого в сумматор в зависимости от значения цифры множителя 
, начиная со старшего разряда, и к сдвигу суммы частичных произведений влево на один разряд.
Умножение начинается со старших разрядов множителя, т.е. множитель сдвигается влево. После каждого такта суммирования сумма частичных произведений сдвигается влево. Множимое остается неподвижным в регистре 
.
Этот вариант технологии умножения отличается от предыдущих тем, что позволяет без значительных затрат оборудования выполнять также и операцию деления, благодаря наличию схем сдвига влево в регистре множителя и в сумматоре частичных произведений.
Технология 4
Запишем произведение в следующем виде:
. (2.8)
Из анализа (2.8) следует, что
,
где 
, а в начале умножения
.
После выполнения 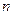циклов умножения в сумматоре сформируется 
.
Функциональная схема реализации рассматриваемой технологии умножения изображена на рис. 2.4.
 |
Рис. 2.4. Четвертая технология умножения
В рассматриваемой технологии каждый цикл умножения сводится к сдвигу множимого на один разряд вправо и к передаче или непередаче его в сумматор в зависимости от цифр множителя 
(0 или 1), начиная со старшего разряда.
Умножение начинается со старших разрядов множителя, т.е. множитель сдвигается влево. После каждого такта суммирования множимое сдвигается вправо. Сумма частных произведений остается неподвижной в сумматоре СМ.
Эта технология выполнения умножения требует для реализации сравнительно большего количества оборудования, однако позволяет сократить время выполнения умножения за счет совмещения во времени тактов суммирования с тактами сдвига множимого.
