Если число 
- неправильная дробь, то в этом случае отдельно переводят целую часть числа и отдельно его дробную часть по изложенным выше правилам. Второй результат приписывают справа к первому, разделив их запятой.
Пример.
Перевести десятичное число 75,364 в двоичную систему счисления, т.е.
75,364(10) (2).
Перевод целой части: Перевод дробной части:
Операция Частное Остаток Операция Целая Дробная
Часть часть
75: 2 = 37 + 1 0,364 х 2 = 0, 728
37: 2 = 18 + 1 0,728 х 2 = 1, 456
18: 2 = 9 + 0 0,456 х 2 = 0, 912
9: 2 = 4 + 1 0,912 х 2 = 1, 824
4: 2 = 2 + 0 0,824 х 2 = 1, 648
2: 2 = 1 + 0 0,648 х 2 = 1, 296
1 и т.д.
Результат перевода неправильной дроби с точностью 
:
75,364(10)=1001011,010111(2).
Частный случай перевода чисел
Из одной системы счисления в другую
Особенно просто перевод чисел из одной системы счисления в другую осуществляется для таких систем, у которых основание одной системы является целой степенью основания другой системы. Выше были рассмотрены две такие системы: двоичная и восьмеричная, у которых соотношения оснований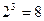 
, и двоичная и шестнадцатеричная, у которых соотношения оснований 
.
Пусть 
и 
- соответственно основания двух позиционных систем счисления, причем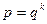 
(
- целые числа). Требуется перевести число 
из -ичной системы в -ичную систему и, наоборот, из -ичной в -ичную систему счисления.
Правила перевода. Для перевода произвольного числа из -ичной системы в -ичную 
необходимо каждую цифру числа в -ичной системе заменить ее
- значным изображением в -ичной системе счисления.
Для перевода произвольного числа 
(в общем случае неправильной дроби) из -ичной системы счисления в -ичную необходимо цифры числа 
слева и справа от запятой разбить на группы по цифр в каждой, дополнив, если это необходимо, крайнюю левую и крайнюю правую группы нулями до цифр в группе и заменив каждую такую - значную группу цифрой в -ичной системе счисления.
Изложенные правила поясним на примерах перевода чисел из восьмеричной системы счисления в двоичную и обратно.
Основание восьмеричной системы 
. Основание двоичной системы 
. Откуда следует, что 
, т.е. 
.
Таким образом, для перевода произвольного восьмеричного числа в двоичную систему счисления следует каждую восьмеричную цифру заменить соответствующим ей трехзначным двоичным числом.
Пример.
Восьмеричное число 
равно двоичному числу 
, т.к. 7=111, 4=100, 3=011, 5=101, 6=110, 1=001.
Для перевода произвольного двоичного числа в восьмеричное систему счисления необходимо, начиная от запятой, разделяющей число на целую и дробную части, влево и вправо от нее разбить набор двоичных цифр, изображающих двоичное число, на тройки цифр. Каждое полученное трехзначное двоичное число отдельно перевести в восьмеричную систему счисления. Если правая и левая группы цифр будут не полными тройками, то их следует дополнить соответственно справа и слева нулями.
Пример.
Двоичное число 
после дополнения его справа и слева нулями до полных троек имеет вид: (001) (101) (110), (011) (111) (010). Эта запись равна восьмеричному числу 
.
Аналогичные преобразования справедливы для перевода двоичных чисел в шестнадцатеричные и наоборот.
Пример.
Двоичное число 
после разбивки его на тетрады слева и справа от запятой принимает вид: (1110) (1101) (1001), (1100) (0111) (1111). Эта запись равна шестнадцатеричному числу 
.
Пример.
Шестнадцатеричное число 
в двоичной системе имеет следующий вид: 
.
Для перевода чисел из восьмеричной системы с счисления в шестнадцатеричную и наоборот необходимо использовать в качестве промежуточной двоичную систему счисления.
