Метод Лемана рассмотрим в предположении, что умножение выполняется, начиная с младших разрядов множителя.
Алгоритм в данном цикле операции умножения может быть записан в следующем виде:
где 
- номер разряда множителя;
- цифра -го разряда множителя;
- двоичная переменная, единичное значение которой для соответствующего разряда множителя указывает на необходимость выполнения арифметического действия между суммой частичных произведений и множимым (сложение или вычитание);
- знак арифметического действия.
Очевидно, что при 
.
Если 
, то производится сложение суммы частичных произведений с множимым. При 
производится вычитание множимого из суммы частичных произведений.
Из анализа приведенных выше выражений, описывающих алгоритм действий в данном цикле умножения, следует, что перед началом операции умножения 
. Это значение сохраняется до появления первой единицы в младшем разряде множителя. При появлении там единицы 
производится сложение множимого с предшествующей суммой частичных произведений, если в следующем по старшинству разряде множителя содержится «0», или производится вычитание множимого из предшествующей суммы частичных произведений, если в следующем по старшинству разряде множителя содержится «1», то есть 
.
При появлении 0 в младшем разряде множителя производится вычитание множимого из предшествующей суммы частичных произведений, если в следующем по старшинству разряде множителя содержится «1» 
, или производится сложение множимого с предшествующей суммой частичных произведений, если в следующем по старшинству разряде множителя содержится «0» 
.
Рассмотрим на конкретном примере последовательность действий в сумматоре и регистре множителя при умножении по методу Лемана.
Пусть множимое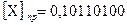 
, а множитель 
.
Будем считать, что множитель и сумма частичных произведений в каждом цикле вычислений сдвигаются на один разряд вправо соответственно в регистре множителя и в сумматоре. Сложение (вычитание) в сумматоре производится в обратном модифицированном коде. Для округления результата в сумматоре имеется дополнительный разряд справа.
С учетом сказанного схема выполнения конкретного примера ускоренного умножения по методу Лемана представлена ниже.
Содержимое Содержимое
регистра 
сумматора 
[CM]
100011 10 исходное состояние 00 00000000 0
010001 11 сдвиг вправо 
и [CM] 00 00000000 0
(-) + 11 01001011 1
11 01001011 1
001000 11 сдвиг вправо и [CM] 11 10100101 1
000100 01 сдвиг вправо и [CM] 11 11010010 1
000010 00 сдвиг вправо и [CM] 11 11101001 0
(+) + 00 10110100 0
1 00 10011101 0
00 10011101 1
000001 00 сдвиг вправо и [CM] 00 01001110 1
000000 10 сдвиг вправо и [CM] 00 00100111 0
000000 01 сдвиг вправо и [CM] 00 00010011 1
(+) + 00 10110100 0
произведение 
00 11000111 1
округление 
00 11001000 0
Непосредственным умножением можно легко проверить, что полученное значение произведения 
соответствует истинному с учетом округления.
Анализ показывает, что при умножении по методу Лемана даже при наиболее неблагоприятном сочетании цифр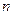 
разрядного множителя (101010…) количество операций суммирования равно 
. В среднем же количество операций суммирования равно 
.
