Любое число в позиционной системе счисления можно представить в следующем виде:
,
где 
- мантисса числа 
, причем 
; 
- нуль или произвольное целое число, называемое порядком числа ; 10 – основание системы счисления.
Например, при двоичной записи мантиссы и порядка имеем:
N1 = + 0,101101 = + 0,101101∙100; (m1 = + 0,101101; p1 = 0);
N2 = – 1101,01 = – 0,110101∙10+100; (m2 = – 0,110101; p2 = +100);
N3 = + 0,000101 = + 0,101000∙10-11; (m3 = + 0,101000; p3 = –11).
Из приведенных примеров легко видеть, что мантисса представляет собой цифровую часть числа, выраженную правильной дробью, а порядок указывает на место положения запятой в числе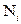 
и является целым числом. Иными словами, порядок указывает номер разряда правильной дроби , после которого при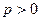 
или перед которым при 
необходимо поставить запятую, начиная счет с первого (старшего) разряда дроби.
Таким образом, для записи числа в ячейке памяти машины с плавающей запятой необходимо иметь место для записи знака мантиссы (знака числа), модуля мантиссы (цифровых разрядов числа ), знака порядка и самого порядка. При этом следует помнить, что весовые коэффициенты цифр мантиссы определяются величиной и знаком порядка, а весовые коэффициенты порядка (разрядов от младшего к старшему) фиксированы и равны 20, 21, 22, 23 и т.д.
Если в старшем разряде мантиссы находится единица, то такое число называется нормализованным, а если в старшем разряде мантиссы или нескольких подряд начиная со старшего разряда мантиссы находятся нули, то такое число называется ненормализованным (денормализованным).
Для его нормализации следует мантиссу сдвинуть влево до первой единицы в старшем разряде, а из порядка отнять число единиц, равное числу разрядов, на которое была сдвинута влево мантисса.
Если при выполнении арифметических операций произойдет переполнение разрядной сетки, т.е. цифровой разряд (старший разряд мантиссы) окажется в знаковом разряде, то мантиссу сдвигают на один разряд вправо и к порядку прибавляют единицу. Эта операция автоматически устраняет переполнение разрядной сетки.
Диапазон нормализованных чисел, представимых в машине с плавающей запятой, может быть определен следующим неравенством:
,
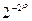
где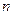 
- число разрядов абсолютной величины мантиссы; 
- число разрядов абсолютной величины порядка.
Столь широкий диапазон представимых чисел делает ненужным при решении задач введение масштабных коэффициентов и практически исключает переполнение разрядной сетки, влекущее за собой останов вычислительного процесса. Однако за эти преимущества приходится платить увеличением числа разрядов в машине, а следовательно, и аппаратурными затратами, а также усложнением системы управления и вычислительных алгоритмов при выполнении арифметических операций, т.е. снижением производительности ЭВМ.
Коды двоичных чисел
В ЭВМ в силу определенных схемотехнических ограничений операция сложение реализуется значительно проще, чем операция вычитание. Поэтому операцию вычитание заменяют операцией сложение специально подобранных кодов, которыми изображаются двоичные числа, являющиеся правильными дробями (положительными или отрицательными).
На практике чаще всего применяются следующие коды: прямой, обратный, дополнительный, модифицированный обратный и модифицированный дополнительный.
Изображения положительных чисел - правильных дробей - совпадает во всех трех кодах (прямом, обратном и дополнительном), а изображения отрицательных чисел - правильных дробей - в соответствующих кодах различается.
Прямой код
Пусть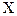 
- правильная двоичная дробь (положительная или отрицательная). В частном случае 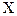равно нулю.
Прямым кодом числа 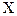называется число, обозначаемое символом 
, получаемое по следующей формуле:
Иными словами, если 
где 
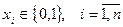, то 
.
Если 
, то 
.
Следовательно, прямой код двоичного числа совпадает по изображению с записью самого числа, при этом в знаковом разряде для положительных чисел записывается 0, а для отрицательных 1.
Пример.
X = + 0,1100111011; [X] np = [+ 0,1100111011] np = 0,1100111011;
X= –0,1100111011; [X] np =[–0,1100111011] np =1–(–0,1100111011)=1,1100111011.
Из определения прямого кода вытекает, что нуль имеет два отвечающих ему значения прямого кода:
[0] np = [+ 0,00…0…0] np = 0,000…0…0;
[0] np = [– 0,00…0…0] np = 1,000…0…0.
Обратный код
Пусть 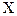– правильная двоичная дробь, в частности 
.
Обратным кодом числа 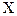называется число, обозначаемое символом 
, получаемое по следующей формуле:
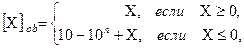
где 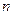- количество цифр (разрядов) дробной части числа 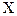; 10 – означает два.
Из определения обратного кода следует, что для положительного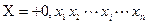 
имеет место совпадение прямого и обратного кодов, т.е. в этом случае
.
Для отрицательного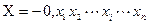 
обратный код образуется следующим образом:
,
где 
, если 
,
, если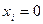 
.
Иными словами, обратный код отрицательного двоичного числа получается следующим образом: в знаковый разряд записывается 1, а значения всех двоичных цифр дробной части инвертируются, т.е. заменяются на противоположные (нуль – на единицу, а единица – на нуль).
Пример.
X = + 0,110011101; [X] ob =[+ 0,1100111011] ob =0,1100111011;
X = – 0,110011101; [X] ob =[– 0,1100111011] ob = 1,0011000100.
Для перевода обратного кода отрицательного числа в прямой код необходимо значение всех цифровых разрядов инвертировать, оставив знаковый разряд без изменения.
Согласно определению обратного кода следует, что для изображения нуля возможны два значения кода:
[0] ob = [ + 0,00…0…0] ob = 0,00…0…0;
[0] ob = [– 0,00…0…0] ob = 1,11…1…1.
