Пусть признак Х некоторой генеральной совокупности распределен по нормальному закону. Генеральная дисперсия неизвестна, но есть основания предполагать, что она равна некоторому значению D 0. Это значение может быть установлено теоретически или по результатам предыдущих опытов. Требуется при определенном уровне значимости проверить гипотезу о равенстве генеральной дисперсии числу D 0.
Рассматриваемая гипотеза чаще всего возникает на практике тогда, когда нужно проверить точность приборов, инструментов, станков, методов исследования и т.д. Например, если известна характеристика D 0 величины отклонения от среднего норматива времени пробега стометровки для положительной оценки, а найденная по выборке исправленная выборочная дисперсия окажется значимо больше, то для группы необходимы дополнительные тренировки.
Рассмотрим общую схему для гипотезы о генеральной дисперсии.
1. Формулируется основная гипотеза  и одна из альтернативных
и одна из альтернативных 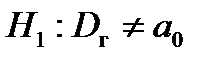 или
или 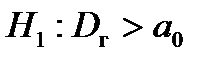 или
или 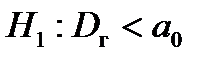 .
.
2. Выбирается уровень значимости α.
3. Выбирается критерий – случайная величина χ 2, распределенная по закону «хи-квадрат» с числом степеней свободы ν = n – 1.
4. Вычисляется выборочное значение критерия 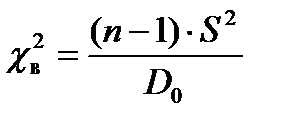 , где n – объем выборки, а S – исправленное среднее квадратическое отклонение.
, где n – объем выборки, а S – исправленное среднее квадратическое отклонение.
5. Выбирается критическая область по альтернативной гипотезе Н 1, а критические точки χ 2кр. по таблице критических точек распределения «хи-квадрат», используя следующую схему
| Альтернативная гипотеза Н 1 | |||||||||||
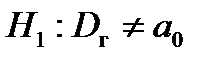
| 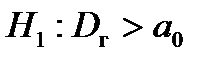
| 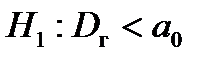
| |||||||||
| V 1 – двусторонняя, несимметричная. | V 1 – правосторонняя | V 1 – левосторонняя | |||||||||
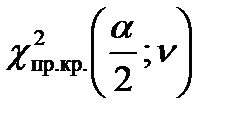 ; ;
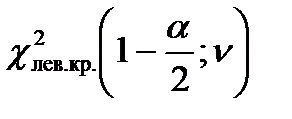 ;
ν = n – 1. ;
ν = n – 1.
|  ν = n – 1.
ν = n – 1.
| 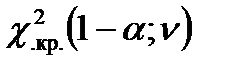 ν = n – 1.
ν = n – 1.
| |||||||||
6. Принимается статистическое решение.
Пример 9.5. Точность работы станка-автомата проверяется по дисперсии контролируемого размера изделий, которая не должна превышать величину 0,1. Взята проба из 25 случайно отобранных изделий и получены следующие результаты измерений:
| Контролируемый размер изделия хi | 3,0 | 3,5 | 4,0 | 4,5 |
| Частоты ni |
Требуется при уровне значимости α = 0,05 проверить гипотезу о том, что станок обеспечивает требуемую точность.
Решение. Применим общую схему.
1.  и, очевидно, что
и, очевидно, что 
2. α = 0,05.
3. Критерий – случайная величина χ 2, распределенная по закону «хи-квадрат» с числом степеней свободы ν = 25 – 1= 24.
4. Выборочное значение 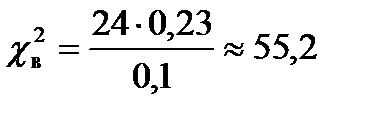 ; так как справедливо следующее
; так как справедливо следующее  ;
;
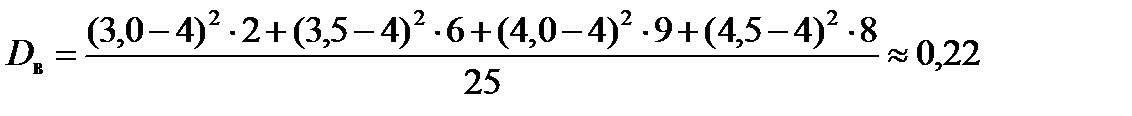 ;
;
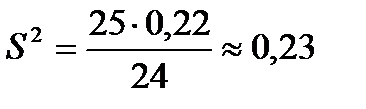 .
.
5. По альтернативной гипотезе  выбираем второй столбец схемы и определяем, что V 1 – правосторонняя критическая область. Критические точки χ 2кр. определяем по таблице критических точек распределения «хи-квадрат»: χ 2кр.(0,05; 24) = 36,4. Строим критическую область и отмечаем на оси выборочное значение
выбираем второй столбец схемы и определяем, что V 1 – правосторонняя критическая область. Критические точки χ 2кр. определяем по таблице критических точек распределения «хи-квадрат»: χ 2кр.(0,05; 24) = 36,4. Строим критическую область и отмечаем на оси выборочное значение
| χ 2кр=36,4 |
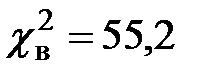
|
6. 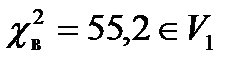 , следовательно, гипотеза Н 0 отвергается, т.е. станок требуемую точность не обеспечивает. ■
, следовательно, гипотеза Н 0 отвергается, т.е. станок требуемую точность не обеспечивает. ■
Рассмотрим еще одну задачу без текстового содержания.
Пример 9.6. Пусть из генеральной совокупности, признак которой распределен по нормальному закону, извлечена выборка объема n = 17. По значениям признака выборочных элементов найдена выборочная дисперсия D в = 0,16. Требуется при уровне значимости α = 0,05 проверить гипотезу о том, что генеральная средняя равна 0,18. В качестве альтернативной рассмотреть две гипотезы о том, что генеральная средняя не равна 0,18 и что меньше 0,18.
Решение. Проверку этой гипотезы проведем также по общей схеме.
1 случай.
1. 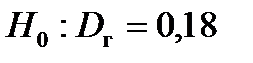 и пусть
и пусть 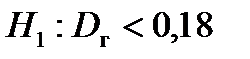
2. α = 0,05.
3. Критерий – случайная величина χ 2, распределенная по закону «хи-квадрат» с числом степеней свободы ν = 17 – 1= 16.
4. Выборочное значение 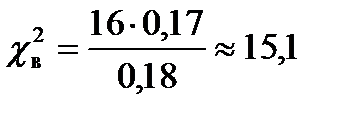 , так как
, так как 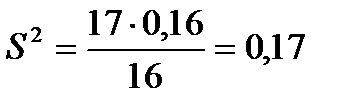 .
.
5. По альтернативной гипотезе 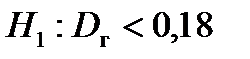 выбираем третий столбец схемы, получаем V 1 – левосторонняя критическая область. Находим критическую точку χ 2кр.(1- 0,05; 16) = χ 2кр.(0,95; 16) = 7,96. Строим критическую область и отмечаем выборочное значение критерия:
выбираем третий столбец схемы, получаем V 1 – левосторонняя критическая область. Находим критическую точку χ 2кр.(1- 0,05; 16) = χ 2кр.(0,95; 16) = 7,96. Строим критическую область и отмечаем выборочное значение критерия:
| χ 2кр=7,96 |

|
6. 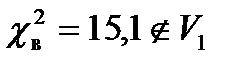 , следовательно, нет оснований отвергнуть гипотезу Н 0.
, следовательно, нет оснований отвергнуть гипотезу Н 0.
2 случай.
1. 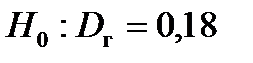 и пусть
и пусть 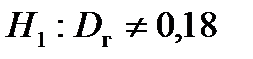
2. α = 0,05.
3. Критерий – случайная величина χ 2, распределенная по закону «хи-квадрат» с числом степеней свободы ν = 17 – 1= 16.
4. Выборочное значение 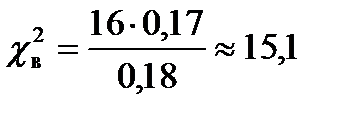 , так как
, так как 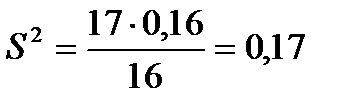 .
.
5. По альтернативной гипотезе 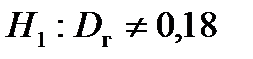 выбираем первый столбец схемы, получаем V 1 – двусторонняя несимметричная критическая область. Находим критические точки
выбираем первый столбец схемы, получаем V 1 – двусторонняя несимметричная критическая область. Находим критические точки
χ 2пр.кр.(0,05/2; 16) = χ 2кр.(0,025; 16) = 28,8;
χ 2лев.кр.(1-0,05/2; 16) = χ 2кр.(0,925; 16) = 6,91.
Строим критическую область и отмечаем выборочное значение критерия:
| 6,91 |
| 28,8 |

|
6. 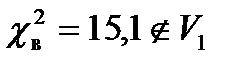 , следовательно, нет оснований отвергнуть гипотезу Н 0.
, следовательно, нет оснований отвергнуть гипотезу Н 0.
Рассмотренными в данной работе гипотезами далеко не исчерпывается список гипотез, необходимость в проверке которых может возникнуть при обработке и анализе статистических данных. Например, особое значение имеют гипотезы о законе распределения признака Х, для проверки которых применяются, так называемые, критерии согласия. Однако их рассмотрение выходит за рамки данного пособия.






