2.1. Для следующих выборок построить дискретные и интервальные вариационные ряды распределения частот и частостей (число интервалов положить равным 3):
а) 3,3,4,6,2,1,6,9,8,10,5,6,4,4,3,3,5,6; б) 1,3,1,6,2,4,6,7,8,11,5,6,1,4,2,3,7,6.
2.2. Для следующих дискретных рядов построить полигон и кумуляту распределения частот и частостей:
| а) | б) | |||||||||
2.3. Для дискретных рядов из примера 2.2 определить выборочную среднюю, моду, медиану, выборочную дисперсию, стандартное отклонение, асимметрию и эксцесс. Дать пояснение найденным статистикам.
2.4. Для следующих интервальных рядов построить полигон, кумуляту и гистограмму распределения частот:
| а) | 1-4 | 4-7 | 7-10 | 10-13 | б) | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 |
2.5. Для интервальных рядов из примера 2.4 определить интервальные статистики: выборочную среднюю, моду, медиану, выборочную дисперсию, стандартное отклонение, асимметрию и эксцесс. Дать пояснение найденным статистикам.
ТЕОРИЯ ОЦЕНИВАНИЯ
Точечные оценки параметров и их свойства
Пусть имеется некоторая генеральная совокупность с изучаемым признаком Х, распределение которого известно, но неизвестны параметры этого распределения, например, неизвестными могут быть математическое ожидание и среднеквадратическое отклонение, если рассматриваемый признак распределен по нормальному закону или неизвестен параметр λ, если признак имеет распределение Пуассона.
Предположим, что для нахождения неизвестных параметров исследовать все элементы генеральной совокупности не представляется возможным. Тогда в результате наблюдения над признаком Х получают выборку объема n, с помощью которой затем находят приближенные значения или оценку неизвестных параметров признака Х.
Функцию, которая дает приближенное значение неизвестного параметра, называют статистической точечной оценкой этого параметра.
Определим более точно понятие точечной оценки.
Понятие точечных оценок
Пусть распределение признака Х генеральной совокупности имеет параметр θ, значение которого неизвестно. Однако существует некоторая формула по которой можно определить приближенно этот параметр, используя значения выборки: х 1, х 2, …, хn. Эти значения можно рассматривать, как частные конкретные значения n независимых случайных величин: X 1, X 2, …, Xn. Каждая из этих величин имеет тот же закон распределения, что и признак Х.
Точечной статистической оценкой 
параметра θ называют всякую функцию результатов наблюдений над случайной величиной Х, с помощью которой можно найти приближенное значение параметра θ.
Оценка определяется как «точечная», потому что она представляет собой число или точку на числовой оси, и как «статистическая», потому что рассчитывается по результатам наблюдений. Все оценки, которые рассматриваются в данном пособии, будут построены по результатам наблюдений, поэтому в дальнейшем слово «статистическая» будем опускать.
Итак, оценка – это некоторая функция случайных величин, т.е.
,
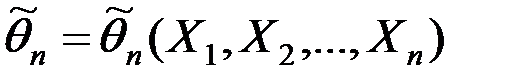следовательно, в отличие от оцениваемого параметра θ, его оценка является также случайной величиной, зависящей от закона распределения признака Х и от объема выборки n. Поясним данный факт более подробно на примере математического ожидания.
Пусть неизвестным параметром θ является математическое ожидание признака Х. Предположим, что в качестве оценки этого параметра предложена средняя арифметическая. Для нахождения приближенного значения параметра произведем выборку объема n и найдем для нее среднюю арифметическую 
. Повторим опыт, получим другую выборку того же объема n и найдем для новой выборки значение средней арифметической 
. Повторяя опыт многократно, будем получать для каждой выборки значение средней арифметической. В результате получим последовательность чисел 
, вообще говоря, различных между собой. Таким образом, оценку можно рассматривать как случайную величину, значениями которой являются средние арифметические различных выборок объема n.
Интерпретация оценки как случайной величины позволяет говорить о ее основных характеристиках: математическом ожидании 
и дисперсии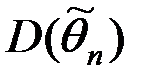 
. С помощью этих характеристик можно сформулировать свойства, которыми должна обладать оценка, чтобы давать наилучшее приближение для неизвестного параметра.
1.2. Основные свойства точечных оценок
Оценка является хорошим приближением для параметра, если она несмещенная, состоятельная и эффективная.
Оценка параметра θ называется несмещенной, если ее математическое ожидание равно оцениваемому параметру при любом объеме выборки, т.е. 
. В противном случае, оценка называется смещенной.
Соблюдение требования несмещенности оценки гарантирует от получения систематических ошибок. Это следует из того, что при 
значения оценки по выборкам будут в среднем завышать истинное значение параметра θ. Если же 
, значения оценок в среднем занижают значение этого параметра.
Предположим теперь, что для некоторого параметра найдены две оценки, причем обе несмещенные. Какую оценку выбрать? Выбирают ту, у которой дисперсия меньше. Если не придерживаться этого правила и выбрать оценку с большой дисперсией, т.е. с большим разбросом значений вокруг математического ожидания, то по данным одной выборки может быть получено значение оценки достаточно далекое от своего математического ожидания, а, следовательно, и от истинного значения параметра. Принимая такую оценку за приближенное значение параметра, получим результат далекий от истины.
Несмещенная оценка параметра θ называется эффективной, если среди всех возможных несмещенных оценок, найденных по выборкам объема n, она имеет наименьшую дисперсию.
В качестве оценок параметров желательно использовать несмещенные и эффективные оценки, что не всегда возможно на практике. Часто для упрощения расчетов используют незначительно смещенные оценки или оценки, у которых дисперсия чуть больше, чем у эффективной оценки. Таким образом, свойства несмещенности и эффективности не являются обязательными для хороших оценок на практике. Однако есть еще одно свойство, которым в первую очередь должна обладать хорошая оценка – это свойство состоятельности.
Оценка параметра θ называется состоятельной, если она сходится по вероятности к оцениваемому параметру при неограниченном увеличении объема выборки, т.е. для любого ε >0 выполняется равенство:
.
Последнее равенство при малых значениях ε означает, что чем больше объем выборки, тем точнее оценка характеризует параметр θ, что полностью согласуется с законом больших чисел. Поэтому на практике используются только состоятельные оценки, для которых практически достоверно, что при больших значениях n выполнено почти точное равенство 
.
