График эмпирической функции распределения для непрерывного вариационного ряда называют кумулятивной кривой или просто кумулятой. Название происходит от английского слова accumulation – накопление.
При нахождении значений функции Fn (x) в числителе записывалась сумма некоторых частот. Эта сумма также имеет свое название – кумулятивная или накопленная частота соответствующего интервала. Дадим более точное определение.
Пусть дан вариационный интервальный ряд распределения частот.
Накопленной частотойniнак. i – го интервала называется сумма частоты данного интервала и частот всех предшествующих интервалов, т.е.
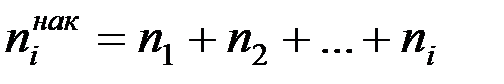 .
.
Нетрудно понять, что накопленная частота последнего интервала совпадает с объемом выборочной совокупности.
Аналогично, для каждого интервала можно определить накопленные частости.
Накопленной частостьюwiнак. i – го интервала называется сумма частости данного интервала и частотей всех предшествующих интервалов, т.е.
 .
.
Ясно, что накопленная частость последнего интервала равна 1.
Определив накопленные частости интервалов, можно иначе определить и кумуляту.
Пусть дан интервальный ряд распределения частостей
| Интервалы | а 1 – а 2 | а 2 – а 3 | … | a m - a m+1 |
| Частости интервалов | w 1 | w 2 | … | w m |
Кумулятой (кумулятивной кривой) интервального ряда распределения частостей называют графическое представление данного ряда в виде ломаной линии, вершины которой находятся в точках с координатами (ai +1; wi), i = 1, 2, …, m, при этом первая точка ломаной находится на оси абсцисс и имеет координаты (а 1; 0).
В качестве графического представления интервального ряда может быть рассмотрена ломаная с вершинами в точках (а 1; 0) и (ai +1; ni), i = 1, 2, …, m. В этом случае полученная кривая будет называться кумулятой распределения частот (а не частостей) интервального ряда.
Общий вид кумулят распределения частот и частостей будет один и тот же. Отличие состоит лишь в масштабе на оси ординат.
Пример 4.5. Для данного интервального ряда построить кумуляту распределения частот и кумуляту распределения частостей
| Интервалы | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 |
| Частоты интервалов |
Решение. Объем статистической совокупности равен n = 20.
Дополним данный интервальный ряд тремя строками. В третьей строке запишем накопленные частоты интервалов, в четвертой – частости, в пятой – накопленные частости интервалов, получим
| Интервалы | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 |
| ni | |||||
| niнак | |||||
| wi | 0,15 | 0,3 | 0,35 | 0,15 | 0,05 |
| wiнак | 0,15 | 0,45 | 0,8 | 0,95 |
| 1 3 5 7 9 11 |
| n iнак |
| x |
Кумулята распределения частостей имеет вид:
| wiнак 0,95 0,8 0,45 0,15 |
| 1 3 5 7 9 11 |
| x |
■
По правилу, связанному с накопленными частотами и частостями, строят кумуляту и для дискретного вариационного ряда. Аналогично определяется накопленная частота и накопленная частость для варианта. Ломаная линия с вершинами в точках (xi, niнак), i = 1, 2, …, m будет определять кумуляту распределения частот дискретного ряда, а ломаная линия с вершинами в точках (xi, wiнак), i = 1, 2, …, m – кумуляту распределения частостей дискретного ряда.
Пример 4. 6. Построить кумуляту распределения частот и кумуляту распределения частостей для следующего дискретного ряда
| Варианты хi | ||||
| Частоты ni |
Решение. Объем статистической совокупности равен n = 10. Дополним данный дискретный ряд тремя строками. В третьей строке запишем накопленные частоты вариантов, в четвертой – частости, в пятой – накопленные частости вариантов, получим
| Варианты хi | ||||
| Частоты ni | ||||
| niнак | ||||
| wi | 0,1 | 0,3 | 0,5 | 0,1 |
| wiнак | 0,1 | 0,4 | 0,9 |
| n i нак |
| х |
| 3 4 6 9 |
и кумуляту распределения частостей:
| wiнак 0,9 0,4 0,1 |
| х |
| 3 4 6 9 |
Для вариационных рядов существуют и другие графические представления.
Полигон распределения
Полигон распределения чаще всего используют для графического представления дискретных рядов.
Пусть дан дискретный ряд распределения частот (частостей).
Полигоном распределения частот дискретного вариационного ряда называется ломаная с вершинами в точках (x i, n i), i = 1, 2, …, m. Для построения полигона распределения частостей вершины ломаной должны находиться в точках (x i, w i), i = 1, 2, …, m.
Пример 4.7. Построить полигон распределения частот и полигон распределения частостей для следующего дискретного ряда:
| Вариант | ||||||
| Частота |
Решение. Объем статистической совокупности равен 20. Дополним ряд одной строкой, где определим для каждого варианта частость, получим
| Вариант | ||||||
| Частота | ||||||
| Частость | 0,15 | 0,2 | 0,3 | 0,25 | 0,05 | 0,05 |
Полигон распределения частот имеет вид:
| n i |
| 2 4 5 8 9 12 |
| x |
Полигон распределения частостей имеет вид:
| w i 0,3 0,25 0,2 0,15 0,05 |
| 2 4 5 8 9 12 |
| x |
■
Очевидно, что полигон распределения частостей дискретного ряда является статистическим (выборочным) аналогом многоугольника распределения дискретной случайной величины.
Для графического представления интервального ряда также может быть построен полигон. Однако вначале интервальный ряд преобразуют в дискретный, для чего каждый интервал заменяют на число, равное середине интервала и ставят в соответствие этому числу частоту (или частость) рассматриваемого интервала. Затем для полученного дискретного ряда строят полигон, который будет являться полигоном и для данного интервального ряда.
Пример 4.8. Построить полигон распределения частот для следующего интервального ряда:
| Интервалы | 2-5 | 5-8 | 8-11 | 11-14 | 14-17 | 17-20 |
| Частоты |
Решение. Объем статистической совокупности равен 16. Дополним таблицу одной строкой. В третьей строке запишем z i – середины соответствующих интервалов, получим
| Интервалы | 2-5 | 5-8 | 8-11 | 11-14 | 14-17 | 17-20 |
| Частоты | ||||||
| z i | 3,5 | 6,5 | 9,5 | 12,5 | 15,5 | 18,5 |
Полигон распределения частот имеет вид:
| 3,5 6,5 9,5 12,5 15,5 18,5 |
| x |
| n i |
■
Из теории вероятностей известно, что для непрерывной случайной величины имеется еще одна форма закона распределения – функция плотности распределения, график которой называется кривой распределения. Рассмотрим статистический аналог этого графика.
Гистограмма распределения
Функция плотности f (x) по определению является производной функции распределения F (x), следовательно, для нее выполнено приближенное равенство
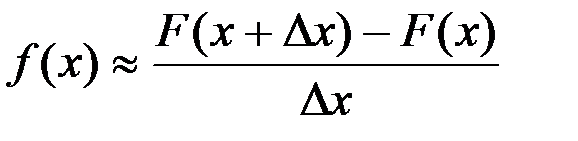 ,
,
при этом, чем меньше Δ х, тем точнее равенство. Естественно, что должен существовать статистический (выборочный) аналог функции плотности и ее графика, который бы характеризовал плотность частости вариантов, расположенных на некотором интервале.
Напомним, что функция плотности имеет место только для непрерывной случайной величины. Рассмотрим ее аналог – непрерывный вариационный ряд:
| Интервалы | а 1 – а 2 | а 2 – а 3 | … | a m − a m+1 |
| Частоты интервалов | n 1 | n 2 | … | n m |
Назовем плотностью распределения частот i – го интервала величину  , где h – это длина интервала, а плотностью распределения частостей i – го интервала величину
, где h – это длина интервала, а плотностью распределения частостей i – го интервала величину  , для i =1, 2, …, т.
, для i =1, 2, …, т.
Гистограммой распределения частот (частостей) называется графическое представление вариационного интервального ряда, представляющее собой ступенчатую фигуру, состоящую из прямоугольников с основаниями, равными интервалам ряда и высотами, равными плотностям распределения частот (частостей).
Пример 4.9. Построить гистограмму распределения частот для следующего интервального ряда:
| Интервалы | 2-5 | 5-8 | 8-11 | 11-14 | 14-17 | 17-20 |
| Частоты |
Решение. Длина любого интервала данного ряда равна h = 3. Дополним данный ряд одной строкой. В третьей строке запишем плотности распределения частот. Получим
| Интервалы | 2-5 | 5-8 | 8-11 | 11-14 | 14-17 | 17-20 |
| Частоты ni | ||||||
| fn (ni) | ≈0,3 | ≈0,7 | ≈1,7 | ≈1,3 | ≈0,7 | ≈0,7 |
| fn 1,7 1,3 0,7 0,3 |
| инт. |
| 2 5 8 11 14 17 20 |
■
Гистограмма распределения частостей отличается от построенного графика лишь выбранным масштабом по оси ординат, сам вид графика остается таким же. Поэтому, несмотря на то, что именно гистограмм распределения частостей является выборочным аналогом кривой распределения (графика функции плотности непрерывной случайной величины), при решении задач часто используется гистограмма распределения частот, как более удобная для исследования.
Более того, так как у рассматриваемых интервальных рядов длины частичных интервалов совпадают, то при построении гистограммы высоту прямоугольников можно выбирать равной частоте (или частости) соответствующего интервала. И в этом случае общий вид графика не изменится, лишь пропорционально изменится высота всех прямоугольников. Заметим, что если длины частичных интервалов интервального ряда не совпадают, то заменять плотность на частоту нельзя.
Обратим внимание на то, что гистограмма распределения частот (если высоты прямоугольников равны частотам, а не плотностям интервалов) тесно связана с полигоном. Если соединить середины верхних оснований прямоугольников прямыми линиями, то в результате получим полигон того же распределения.
В дальнейшем, если не будет особо указано, при решении задач можно использовать любой вид гистограммы.






