Предположим, что по результатам выборки получена оценка 
неизвестного параметра θ. Очевидно, что эта оценка тем точнее будет определять значение параметра, чем меньше величина 
. Если указать некоторое положительное число δ, для которого выполнено неравенство
, (7.1)
то это число будет характеризовать точность оценки . Чем меньше значение δ, тем точнее оценка . Однако нельзя категорически утверждать, что для какой-нибудь оценки будет выполнено неравенство (7.1). Так как оценка – величина случайная, то можно говорить только о вероятности, с которой это неравенство будет выполнено.
Доверительной вероятностью, уровнем доверия или надежностью γ оценки параметра θ называют вероятность γ, с которой осуществляется неравенство (7.1), т.е.
. (7.2)
В практических задачах доверительную вероятность задают в самом начале решения и, естественно, в качестве ее значения берут число, близкое к единице, например, 0,95; 0,99; 0,999 и т.п.
Достаточно часто используется другой вид формулы для доверительной вероятности, а именно
(7.3)
Формула (7.3) получается из формулы (7.2) в результате простых преобразований неравенства в скобках (раскрытием модуля и прибавлением ко всем частям неравенства величины ). Если в последней формуле обозначить через 
и 
, то формула (7.3) примет вид:
(7.4)
Интервальной оценкой или доверительным интервалом параметра θ называют числовой интервал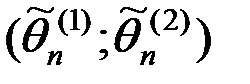 
, который с заданной вероятностью γ накрывает неизвестное значение параметра θ.
Границы доверительного интервала называются доверительными границами.
Необходимо отметить, что слова «накрывает неизвестное значение параметра» в определении интервальной оценки не совсем верно заменять словами «неизвестное значение параметра попадет в заданный интервал». Это связано с тем, что границы доверительного интервала являются случайными величинами (принимают свое значение в зависимости от выборки и доверительной вероятности), а сам неизвестный параметр – величина постоянная.
И, наконец, очень часто границы доверительного интервала расположены симметрично относительно точечной оценки параметра, как при вышеописанном построении. Однако не всегда и не для всех задач можно построить доверительный интервал с таким свойством.
Построение интервальных оценок связано с формулами вероятности попадания значений случайной величины (значения признака Х) на заданный интервал. Формулы, в свою очередь, связаны с конкретным законом распределения соответствующей случайной величины, например с функцией распределения. Построим интервальную оценку для генеральной средней наиболее часто встречающегося закона – нормального закона распределения.
2.3. Доверительный интервал для генеральной средней
Предположим, что признак Х генеральной совокупности распределен по нормальному закону, при этом неизвестен параметр этого распределения – генеральная средняя. Как известно, нормальный закон распределения характеризуется двумя параметрами: математическим ожиданием (генеральной средней) и дисперсией или средним квадратическим отклонением. Доверительный интервал для генеральной средней будем строить для двух случаев, когда известно и неизвестно среднее квадратическое отклонение признака Х генеральной совокупности.
Доверительный интервал для генеральной средней 
при известном среднеквадратическом отклонении 
.
Из генеральной совокупности произведем различные выборки объема n. Для каждой выборки может быть найдена своя выборочная средняя. Эти выборочные средние будем рассматривать как значения некоторой случайной величины 
. Примем без доказательства тот факт, что если случайная величина (признак) Х распределена по нормальному закону, то случайная величина , значения которой определяются по независимым наблюдениям как выборочные средние, также распределена нормально. Этот факт непосредственно следует из теоремы Ляпунова.
По результатам наблюдений найдем точечную оценку неизвестного параметра - выборочную среднюю 
. Зададим доверительную вероятность γ и найдем такое число δ > 0, чтобы выполнялось условие (см. формулу (7.2))
.
Как известно, для нормально распределенной величины Х вероятность попадания на некоторый интервал определяется с помощью функции Лапласа Ф (u). С учетом равенства (6.4) в наших обозначениях формула для определения вероятности примет вид:
.
Последнее равенство следует из формулы (6.6): 
.
Пусть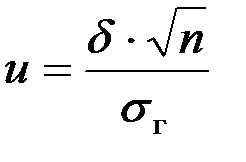 
. Отсюда 
и формула для определения соответствующей вероятности примет вид:
(7.5)
Запишем равенство (7.5) для конкретного значения случайной величины - выборочной средней, получим
(7.6)
Вспомнив о том, что это вероятность равна γ, равенство (7.6) можно интерпретировать следующим образом: с вероятностью γ можно утверждать, что доверительный интервал
(7.7)
покрывает значение генерального среднего; точность полученной оценки
(7.8)
Исследуя формулу (7.8) для нахождения точности оценки, можно сделать следующие выводы:
1. При возрастании объема выборки n точность оценки увеличивается, так как чем меньше значение δ, тем выше точность.
2. Увеличение надежности оценки приводит к уменьшению ее точности. Это следует из того, что функция Лапласа является возрастающей и при увеличении значения этой функции (надежности) ее аргумент также увеличивается, что приводит к увеличению значения δ и понижению точности оценки.
Нахождение доверительного интервала для генеральной средней при известном генеральном среднем квадратическом отклонении можно проводить по следующей схеме:
1. Задать доверительную вероятность γ.
2. Найти по таблице значений функции Лапласа Ф (u) аргумент u, для которого Ф (u) =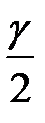 
.
3. Определить точность оценки по формуле .
4. Найти по выборке выборочную среднюю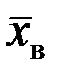 
(если она не дано).
5. Построить доверительный интервал 
Пример 7.1. Пусть признак Х генеральной совокупности распределен по нормальному закону с известным средним квадратическим отклонением σ г = 2 и неизвестной генеральной средней. По случайной повторной выборке объема n = 36 найдена выборочная средняя 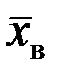= 20. Найти с надежностью γ = 0,95 интервальную оценку для неизвестного параметра, а также точность этой оценки.
Решение. Находить оценку будем по предложенной выше схеме.
1. Доверительная вероятность γ = 0,95.
2. По таблице значений функции Лапласа находим аргумент u, для которого Ф (u) = 0,475. Получаем u = 1,96.
3. Определяем точность оценки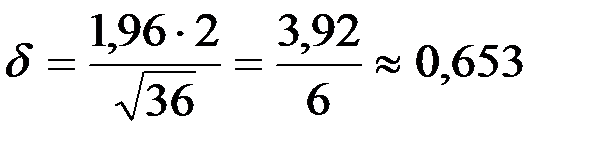 
.
4. Выборочная средняя 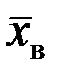= 20.
5. Строим доверительный интервал (20 – 0,653; 20 + 0,653) и окончательно получаем (19,347; 20,653).
Таким образом, с вероятностью 0,95 (или 95%) можно быть уверенным в том, что интервал (19,347; 20,653) накроет значение генеральной средней или с этой же вероятностью можно быть уверенным в том, что выборочное среднее дает значение генеральной средней с точностью 0,653. ■
Пример 7.2. При 25 контрольных испытаниях на продолжительность работы некоторого прибора была определена средняя продолжительность 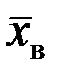=1000 часов. Считая, что продолжительность работы прибора распределена нормально с генеральным средним квадратическим отклонением равным 12 часам, определить:
- доверительный интервал для генеральной средней с точностью оценки, равной 8 часам;
- доверительную вероятность того, что средняя выборочная будет определять генеральную среднюю с точностью 8 часов.
Решение. Очевидно, что доверительный интервал при заданной точности оценки равен (1000 – 8; 1000 + 8), т.е. (992; 1008).
Из формулы (6.10) получаем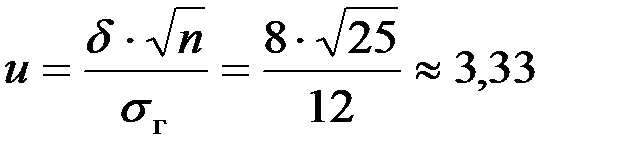 
. По таблице значений функции Лапласа находим Ф (3,33) ≈ 0,49931. Отсюда γ = 0,99862.■
Пример 7.3. Найти минимальный объем выборки из генеральной совокупности с нормально распределенным признаком Х, при котором с вероятностью не меньшей γ = 0,9, отклонение средней, найденной по этой выборке, от генеральной средней будет меньше 0,4, если генеральное среднеквадратическое отклонение равно 3.
Решение Из условия задачи известно, что γ = 0,9; σ г = 3; δ = 0,4. Формула (7.2) для данных примера примет вид: 
. Необходимо отметить следующее: при заданных значениях σ г и δ с ростом объема выборки n увеличивается и надежность γ. Поэтому неравенство 
выполняется для 
. Найдем значение правой части последнего неравенства. Для этого по таблице значений функции Лапласа определим аргумент u, для которого Ф (u) = 0,9/2 = 0,45. Получим u = 1,65. Далее подставляем все значения в неравенство для определения наименьшего значения n, получим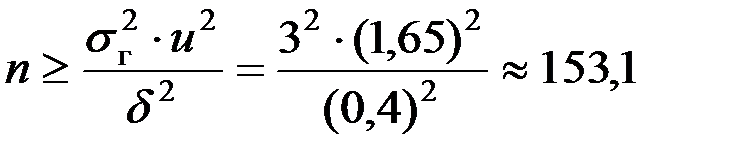 
. Следовательно, минимальный объем выборки n = 154.■
Итак, задача построения интервальной оценки для генеральной средней при известном генеральном среднеквадратическом отклонении решена. Решим теперь эту же задачу в том случае, когда среднеквадратическое отклонение признака генеральной совокупности неизвестно.
Доверительный интервал для генеральной средней при неизвестном среднеквадратическом отклонении .
Пусть некоторый признак Х генеральной совокупности распределен нормально с неизвестными параметрами: и . требуется оценить генеральную среднюю.
Как и в предыдущем случае, из генеральной совокупности будем производить повторные выборки объема n. Для каждой выборки фиксируем выборочную среднюю и исправленное выборочное среднеквадратическое отклонение. Напомним, что исправленное выборочное среднеквадратическое отклонение является достаточно хорошей оценкой для генерального среднеквадратического отклонения. Пусть 
- это случайная величина, значениями которой являются выборочные средние, а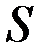 
- случайная величина, значениями которой являются исправленные выборочные среднеквадратические отклонения. Примем без доказательства следующую теорему.
Теорема 7.1. В сделанных выше обозначениях случайная величина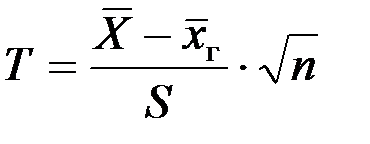 
распределена по закону Стьюдента с (n – 1) –ой степенью свободы.
Для определения вероятности попадания случайной величины, распределенной по закону Стьюдента, на заданный интервал используют таблицу значений t распределения Стьюдента. Тогда, воспользовавшись указанной таблицей, для заданной доверительной вероятности γ и заданного числа степеней свободы ν = n – 1 можно найти такое значение t, при котором выполняется неравенство: 
. Подставим в полученное неравенство T из теоремы, получим 
. Преобразуем левую часть 
Отсюда, следует равенство:
(7.9)
Заменив в равенстве (7.9) случайные величины и 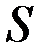их конкретными выборочными значениям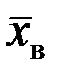и и 
, получим формулу
(7.10)
Таким образом, доверительным интервалом для генеральной средней нормально распределенного признака Х при неизвестном генеральном среднем квадратическом отклонении является интервал
, (7.11)
где величина t определяется по таблице значений распределения Стьюдента с вероятностью γ и числом степеней свободы ν = n – 1.
Пример 7.4. При 25 контрольных испытаниях на продолжительность работы некоторого прибора была определена средняя продолжительность 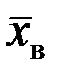=2000 часов и среднее квадратическое отклонение 
=20 часов. Считая, что продолжительность работы прибора распределена нормально, определить доверительный интервал для генеральной средней с надежностью 0,9.
Решение. Для нахождения доверительного интервала по формуле (7.11) найдем величины t и s.
По таблице распределения Стьюдента для вероятности 
и числа степеней свободы 
находим t = 1,71. Исправленное среднеквадратическое отклонение находим по формуле 
. Подставим найденные и данные в условии задачи значения в формулу (7.11), получим
.
Итак, с доверительной вероятностью 0,9 можно считать, что доверительный интервал (1993,02; 2006,98) накроет неизвестную генеральную среднюю. ■
