Допустим, что выполняется серия из n независимых одинаковых испытаний. Испытания независимы в том смысле, что результаты одних испытаний не влияют на результаты других. В каждом испытании может появиться или не появиться некоторое случайное событие А. Будем предполагать, что вероятность появления события А в одном испытании одна и та же, т.е. не зависит от номера испытания. Традиционно принято называть исход, при котором появляется событие А – «успехом», а исход, при котором не появляется событие
А – «неудачей».
Одинаковые независимые испытания называются испытаниями Бернулли, если в каждом испытании возможны только два исхода («успех» и «неудача»)
и вероятности каждого из этих исходов постоянны, т.е. не меняются от испытания к испытанию.
Обозначим через р – вероятность «успеха», т.е. появления события А в одном испытании, а именно, р = Р (А); q – вероятность «неудачи», т.е. непоявления события А в одном испытании, а именно, q = Р (Ā).
Тогда, очевидно, р + q = 1 или q = 1 – р.
Итак, для того, чтобы n одинаковых испытаний назывались испытаниями Бернулли, необходимо выполнение трех условий:
1. Испытания должны быть независимыми.
2. В каждом испытании возможно только два исхода («успех» и «неудача»).
3. Вероятность «успеха» р в каждом испытании постоянна, т.е. не зависит от номера испытания. (Очевидно, что q также не зависит от номера испытания.)
Так как вероятность появления события А в одном испытании известна и равна р, то естественно возникают вопросы, а чему равна вероятность появления события А, к примеру т раз в n испытаниях или не менее т раз в n испытаниях? Попытаемся ответить на эти вопросы.
Пусть 
– вероятность появления события А ровно т раз в n испытаниях;
– вероятность появления события А не менее т раз в n испытаниях.
Допустим, что интересующее нас событие А появилось в первых т испытаниях и не появилось в остальных n – т. Вероятность такой ситуации по теореме умножения для независимых событий равна 
.
Разумеется, возможен и иной порядок появления события А. Например, оно может не появиться в первых n – т испытаниях, а появиться в последних т испытаниях. Вероятность такого варианта равна 
или .
Возможны и другие варианты. Всего таких вариантов столько, сколько имеется сочетаний из n элементов по т, т.е.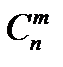 
. Каждый из вариантов имеет одну и ту же вероятность .
Для нас безразлично, в какой последовательности появляется событие А. Важно, чтобы оно появилось в каких-то т испытаниях и не появилось в остальных n – т испытаниях. Поэтому
(18)
Формула (10.18) носит название формулы Бернулли.
Рассмотрим частные случаи формулы (10.18).
1.Вероятность того, что событие А появится во всех n испытаниях равна
. (19)
2.Вероятность того, что в n испытаниях событие А не появиться ни разу равна
. (20)
3.Вероятность того, что в n испытаниях событие А появится не менее т раз равна
. (21)
4.Вероятность того, что в n испытаниях событие А появится не менее т 1 раз и не более т 2 раз равна
. (22)
Заметим, что для всех n испытаний Бернулли выполнено следующее равенство 
.
Пример 17. Расход электроэнергии на протяжении суток не превышает установленной нормы с вероятностью р = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии не будет превышать нормы в течение четырех суток.
Решение. Испытанием будем считать расход электроэнергии в течение суток. Событие А означает отсутствие перерасхода энергии в течение одних суток, тогда 
Применяя формулу (10.18), получим
. ■
Пример 18. Вероятность попадания в цель для стрелка равна 0,6. Какова вероятность из 10 выстрелов:
1) попасть ровно 4 раза;
2) попасть не менее 8 раз;
3) попасть не менее 3 раз.
Решение. Испытание – выстрел в цель. Событие А означает попадание в цель при одном выстреле, тогда событие Ā – не попадание в цель при одном выстреле. Отсюда 
1) Используем формулу (10.18), получим:
.
2) Используем формулу (10.21), получим:
3) Данную задачу легче решить, если перейти к противоположному событию, т.е. 
. ■
Пример 19. Что вероятнее: выиграть у равносильного противника четыре партии из пяти или семь партий из девяти?
Решение. Пусть событие А означает, что выиграет, например, первый игрок. Так как противники равносильны, то вероятность выигрыша и проигрыша для каждого игрока одинаковы, т.е. 
Получим 
Таким образом, вероятнее выиграть 4 партии из 5, чем 7 из 9. ■
Рассмотрим n испытаний Бернулли с вероятностью успеха р.
Число т 0 наступлений события А называется наивероятнейшим, если вероятность того, что событие А наступит в этих испытаниях т 0 раз, превышает или, по крайней мере, не меньше вероятности остальных возможных исходов испытаний.
Можно показать, что наивероятнейшее число определяется из двойного неравенства:
(23)
причем, если
1) число 
– дробное, то существует одно наивероятнейшее число,
которое равно ближайшему целому, большему ;
2) число – целое, то существуют два наивероятнейших числа, равных и 
.
Пример 20. Отдел технического контроля проверяет партию, состоящую из 20 деталей. Вероятность того, что выбранная случайным образом деталь будет стандартной, равна 0,7. Найти наивероятнейшее число деталей, которые будут признаны стандартными.
Решение. По условию задачи n = 20, p = 0,7; q = 0,3. Отсюда 
и 
.
Итак, по формуле (10.23) получим 
, следовательно, наивероятнейшее число равно 
. ■
Решение задач с применением формулы Бернулли не вызывает особых трудностей, если число испытаний n невелико. При больших значениях n целесообразно для определения соответствующей вероятности применять приближенную формулу, о которой идет речь в локальной предельной теореме.
