Теорема Бернулли. Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р. Тогда для любого ε >0, будет выполнено неравенство
,
где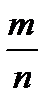 
- относительная частота появления события А.
Теорема Бернулли устанавливает связь между вероятностью появления события и относительной частотой его появления. Кроме этого, она позволяет при этом предсказать, какой примерно будет эта частота в n испытаниях.
Смысл теоремы Бернулли состоит в том, что при большом числе повторных независимых испытаний, в каждом из которых возможно появление события А, практически достоверно, что относительная частота появления этого события (случайная величина) как угодно мало отличается от некоторой неслучайной величины – вероятности события А. Таким образом, в этой ситуации относительная частота перестает быть случайной.
Теорема Бернулли дает теоретическое обоснование для статистического определения вероятности некоторого события и позволяет обосновать широкое применение на практике вероятностных методов исследования.
При доказательстве теоремы Бернулли выводится неравенство, которое часто применяется на практике.
Следствие 3. Если вероятность события А в каждом из n независимых испытаний постоянна и равна р, то при достаточно большом n для произвольного положительного ε справедливо неравенство
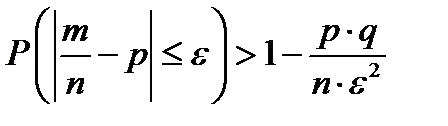, (1.7)
где m – число появлений события А в n испытаниях, q =1- p.
Пример 1.3. При штамповке пластинок из пластмассы брак составляет 3%. Оценить вероятность того, что при проверке партии в 1000 пластинок выявится отклонение от установленного процента брака меньше чем на 1%.
Решение. Из условия задачи следует, что n =1000; ε =0,01; р =0,03; q =1- р =0,97. Применяя формулу (1.7), получим
.
Таким образом, вероятность будет не меньше 0,709. ■
Пример 1.4. При каком числе независимых испытаний вероятность выполнения неравенства 
превысит 0,96, если вероятность появления события в отдельном испытании р =0,7?
Решение. По условию задачи имеем ε =0,2; р =0,7; q =1- р =0,3. Требуется определить n с помощью неравенства (1.7). Условие Р >0,96 равносильно неравенству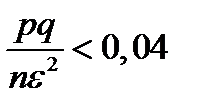 
, откуда 
.
Следовательно, требуется 132 испытания. ■
Теорема Бернулли имеет обобщение в виде теоремы Пуассона, в которой предполагается, что вероятности событий в каждом испытании могут быть различны.
Теорема Пуассона. Пусть производится n независимых испытаний, в каждом из которых вероятности появления события А равны р 1, р 2, …, р n соответственно. Тогда для любого ε >0, будет выполнено неравенство
, (1.8)
где 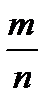- относительная частота появления события А.
Теорема Пуассона значительно реже применяется на практике, чем теорема Бернулли. Однако она незаменима при нахождении приближенного значения средней вероятности события А в серии опытов, если при проведении этой серии одинаковость условий трудно гарантировать.
