Пусть рассматривается некоторое испытание, в котором возможно появление случайного события А. Если кроме условия испытания никаких ограничений для события А не существует, то вероятность события А называют безусловной вероятностью. Если же задаются некоторые дополнительные условия, то появляется условная вероятность этого события. Чаще всего дополнительные условия связаны с появлением другого случайного события.
Итак, при анализе того или иного явления может возникнуть вопрос: влияет ли на возможность появления некоторого события А наступление другого случайного события В и если влияет, то как? Например, наступление В ведет к обязательному наступлению события А или, наоборот, исключает возможность появления события А, а может быть лишь изменяет значение вероятности. Легко понять, что если событие В является благоприятствующим событию А, то при наступлении события В событие А всегда наступает, или если А и В – два несовместных в данном испытании события, то при наступлении события В событие А никогда не будет происходить. Однако это так называемые крайние случаи. Наибольший интерес возникает тогда, когда наступление события В как-то изменяет (увеличивает или уменьшает) вероятность появления события А, не превращая его в достоверное или невозможное при новых условиях событие.
Характеристикой такого влияния одного события на другое служит условная вероятность.
Условной вероятностью 
события А при условии В называется
вероятность события А, вычисленная в предположении, что событие В уже произошло.
Аналогично можно определить условную вероятность 
события В, при условии, что событие А уже произошло.
Пример 12. Пусть в урне находятся 6 белых и 8 черных шаров. Из урны последовательно друг за другом случайным образом вынимают два шара, не возвращая их обратно. Найти вероятность того, что второй шар окажется белым, если первым был вынут также белый шар?
Решение. Пусть событие А состоит в том, что второй шар окажется белым, а событие В, что первый шар белый. В задаче требуется найти вероятность события А, при условии, что событие В произошло, т.е. найти 
. Если событие В произошло, то в урне осталось 13 шаров, из которых 5 белых. Следовательно, вероятность вынуть белый шар из 13, среди которых 5 белых равна 
. ■
Отметим два момента.
Во-первых, для события А может быть найдена не только его условная
вероятность, но и так называемая полная вероятность события, т.е. вероятность того, что второй шар окажется белым при выборе первым любого шара. О нахождении такой вероятности речь пойдет позже.
Во-вторых, условие примера может быть так изменено, что цвет первого выбранного шара вообще не будет влиять на вероятность появления события А. Будем считать, что шары после фиксирования их цвета возвращаются обратно в урну. Тогда, очевидно, вероятность события А не зависит от того, какого цвета был выбран первый шар, т.е. от появления (или не появления) события В.
В этом случае 
, т.е. вероятность события А совпадает
с условной вероятностью этого события. Сами же события А и В являются
независимыми в данном испытании.
Два события А и В называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае, события называются зависимыми.
Из определения следует, что для независимых событий А и В справедливы формулы:
(10)
Для зависимых событий можно доказать следующую формулу
(11)
Необходимо обратить внимание на то, что знаменатель в формуле (10.11) отличен от нуля, так как по условию событие В может произойти, т.е. тВ не равно нулю.
Также можно получить формулу для условной вероятности события В: 
. Но, так как событие АВ ничем не отличается от события ВА и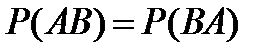 
, то условную вероятность события В можно определить по формуле
(12)
Из формул (11) и (12) непосредственно вытекает следующая теорема умножения вероятностей.
Теорема 7. Вероятность одновременного появления двух случайных
событий равна произведению вероятности одного события на условную вероятность другого, вычисленную в предположении, что первое событие уже
наступило, т.е.
(13)
Следствие. Вероятность одновременного появления нескольких случайных событий равна произведению вероятности одного события на условные вероятности всех остальных, при этом вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились, т.е.
.
Пример 13. В лотереи находятся 20 билетов, из которых 5 выигрышных. Случайным образом выбирают последовательно друг за другом 3 билета без возвращения. Определить вероятность того, что первый, второй и третий билеты будут выигрышными.
Решение. Пусть событие А состоит в том, что первым выберут выигрышный билет, событие В – в том, что второй билет будет выигрышным и, наконец, С – третий билет выигрышный. Очевидно, что 
.
Условная вероятность события В при условии, что событие А произошло, т.е. из лотереи был выбран один выигрышный билет, равна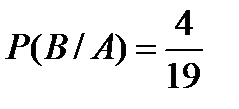 
(всего билетов осталось 19, из них 4 выигрышных).
Условная вероятность события С при условии, что события А и В произошли, т.е. были выбраны два выигрышных билета, равна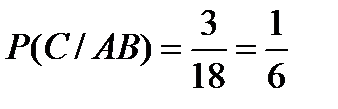 
.
По следствию к теореме вероятность произведения равна
. ■
Теорема 7 верна для любых случайных событий А и В. В частном случае, когда события А и В являются независимыми справедливо следующее утверждение.
Теорема 8. Вероятность одновременного появления двух несовместных событий А и В равна произведению вероятностей этих событий, т.е.
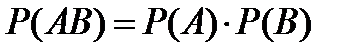(14)
Верно и обратное утверждение.
Теорема 9. Если для двух событий верна формула (14), то эти события независимы.
Основные теоремы теории вероятностей существенно используются при выводе очень важных утверждений, носящих названия формулы полной вероятности и формул Байеса.
