Комбинации элементов могут быть составлены различными способами, а именно, в виде перестановок, размещений и сочетаний. Прежде чем перейти к рассмотрению этих понятий, познакомимся с понятием факториала натурального числа.
Факториалом натурального числа n называется произведение всех натуральных чисел до n включительно, т.е.
.
Например, 1!=1
2!= 1·2=2
3!= 1·2·3=6
4!= 1·2·3·4=24 и т.д.
По определению принято, что 0! = 1.
Пусть имеется три различных элемента a, b, c. Будем составлять из этих элементов различные комбинации.
Размещения
Выберем из трех элементов a, b, c два элемента с учетом их расположения. Получим a b, b a, b c, c b, a c, c a.
Составленные комбинации называются размещениями из трех элементов по два.
Размещениями из n элементов по т в каждом называются такие комбинации из т элементов, взятых из n элементов, которые отличаются друг от друга либо самими элементами, либо порядком их расположения.
Например, размещения a b и b a отличаются порядком расположения элементов, а размещения a b и c b отличаются элементами a и c.
Очевидно, что т ≤ n.
На практике чаще представляют интерес не сами размещения, а их число. Для того чтобы понять формулу для числа размещений рассмотрим следующий пример.
Пример 6. Руководство некоторого банка должно выбрать трех человек из 12 на три различные должности. Все 12 кандидатов имеют равные шансы на занятие той или иной должности. Сколько существует всевозможных вариантов для выбора?
Решение. Используем правило умножения. Первого человека нужно выбрать из 12 кандидатов, следовательно, существует 12 способов выбора, второго человека выбирают из оставшихся 11, поэтому для осуществления второго действия имеется 11 способов. И, наконец, третьего человека выбираем из оставшихся десяти. Очевидно, что число способов осуществления третьего действия равно 10. По правилу умножения можно составить 12·11·10 =1320 различных вариантов по 3 человека в каждом.
С другой стороны, число всевозможных вариантов выбора равно числу размещений из 12 человек по три. Очевидно, что комбинации, состоящие из трех человек, будут размещениями, так как они будут отличаться либо самими людьми, либо расположением этих людей соответственно их должностям
(по условию примера – должности разные). Таким образом, число размещений из 12 человек по 3 равно 12·11·10=1320.■
Теорема 1. Число размещений из n элементов по т вычисляется по следующей формуле
(3)
где 
.
Формула (3) может быть преобразована к более удобному виду.
Теорема 10.2. Число размещений из n элементов по т может быть вычислено по следующей формуле
(4)
В условии предыдущих примеров предполагалось, что 
. Рассмотрим отдельно случай, когда 
. Соответствующие этому случаю размещения называются перестановками.
Перестановки
Выберем из трех элементов a, b, c три элемента с учетом их расположения. Получим a b с, b a с, b c а, c b а, a c b, c a b.
Составленные комбинации называются перестановками из трех элементов.
Перестановками из n элементов называются комбинации, которые состоят из всех n элементов и отличаются лишь порядком расположения этих элементов.
Иначе, перестановки – это размещения из n элементов по n. Нетрудно
получить формулу для числа перестановок.
Теорема 3. Число перестановок из n различных элементов равно
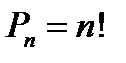(5)
Пример 7. Представитель торговой фирмы ежедневно просматривает
4 изданий, в которых исследуется спрос и предложение на определенные товары. Сколько существует способов просмотра, если выбор изданий случаен?
Решение. Каждый день все 4 изданий должны быть просмотрены, может меняться лишь порядок просмотра, поэтому число способов просмотра равно 
. ■
Рассмотрим два различных размещения, которые состоят из одних и тех же элементов. Тогда они обязательно должны отличаться порядком расположения этих элементов.
Однако часто бывает, что нет необходимости учитывать этот порядок, т.е. размещения, которые отличаются лишь расположением элементов считать равными.
Сочетания
Выберем из трех элементов a, b, c два элемента без учета их расположения. Получим a b, b c, a c.
Составленные комбинации называются сочетаниями из трех элементов по два.
Сочетаниями из n элементов по т в каждом называются такие комбинации т элементов, взятых из n элементов, которые отличаются друг от друга по крайней мере одним элементом.
Очевидно, что т ≤ n.
Теорема 4. Число сочетаний из n элементов по т определяется по следующей формуле
(6)
где .
Пример 8. Решить пример 4, предполагая, что кандидаты выбираются на одинаковые должности.
Решение. В виду того, что должности одинаковые, то порядок выбора кандидатов значения не имеет, поэтому при решении применяем формулу для числа сочетаний, получаем 
.■
Покажем применение классического определения и формул комбинаторики для нахождения вероятности случайных событий.
Пример 9. Найти вероятность того, что в игре «Спортлото» 6 из 49 будет отгадано ровно три номера.
Решение. Ясно, что n равно числу способов выбора 6 номеров из 49, т.е. 
.
По условию примера событие А, вероятность которого надо найти, означает, что из шести выбранных номеров три отгадано верно и три не отгадано.
Таким образом, 
.
Следовательно, 
■.
При решении задач теории вероятностей часто используются ее основные теоремы, связанные с нахождением вероятностей суммы и произведения событий.
