Рассмотрим следующую задачу.
Пример 14. В трех одинаковых ящиках находятся: в первом – 3 белых и 2 черных шара, во втором – 6 белых и 4 черных шара, в третьем – 2 белых и 3 черных шара. Из случайно выбранного ящика наугад вынимается шар. Какова вероятность того, что этот шар белый?
Решение. Пусть событие А означает, что вынутый шар белый. Нетрудно видеть, что вероятность этого события зависит от того, из какого ящика вынимается шар, так как количество белых и черных шаров в ящиках различно.
В связи с этим введем в рассмотрение следующие события:
Н 1 – шар вынут из первого ящика;
Н 2 – шар вынут из второго ящика;
Н 3 – шар вынут из третьего ящика.
Так как ящиков только три, то ясно, что события Н 1, Н 2 и Н 3 образуют полную группу (события несовместны, так как выбирается один шар, и в результате испытания: выбор одного шара, одно из этих событий обязательно произойдет). Кроме этого, эти события равновероятны, так как возможность выбора ящика с последующим взятием из него шара одинакова для всех трех ящиков. Таким образом, 
.
Событие А по условию задачи должно произойти с одним из событий Н 1, Н 2 или Н 3 (шар должен быть вынут либо из первого, либо из второго, либо из третьего ящика). Используя алгебру событий можно событие А записать в следующем виде: 
.
Последнее равенство по сути означает, что событие А произойдет тогда, когда белый шар будет вынут из первого ящика (Н 1 А) или белый шар будет вынут из второго ящика (Н 2 А) или белый шар будет вынут из третьего ящика (Н 3 А). Найдем вероятность события А, получим
.
Последнее равенство следует из очевидной несовместности событий Н 1 А, Н 2 А и Н 3 А. Применим далее теорему умножения вероятностей, тогда
.
Так как событие А / Н 1 означает, что выбран белый шар при условии, что его выбирают из первого ящика, то вероятность этого события по классической формуле равна 
. Аналогично можно найти 
и 
. Окончательно получаем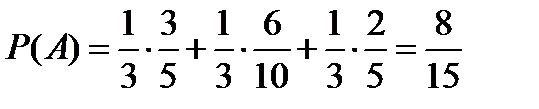 
. ■
В рассмотренном примере по существу приведен вывод так называемой формулы полной вероятности.
Теорема 10. Пусть Н 1, Н 2, …, Нn – полная группа событий для некоторого испытания и событие А может произойти вместе с одним из событий полной группы. Тогда справедлива формула
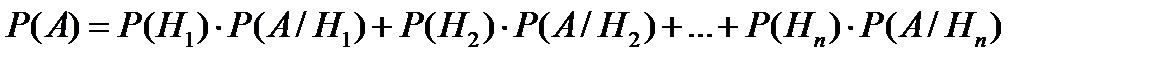(10.15)
Формула (10.15) носит название формулы полной вероятности, а события Н 1, Н 2, …, Нn называются гипотезами.
Формула полной вероятности применяется в тех случаях, когда само испытание как бы распадается на два этапа: на первом этапе определяются возможные условия опыта, т.е. гипотезы, на втором происходит сам опыт одновременно с какой-то гипотезой.
Пример 15. Для приема зачета преподаватель подготовил 50 задач:
20 задач по дифференциальному и 30 задач по интегральному исчислению. Для получения зачета студент должен решить первую попавшуюся ему задачу.
Какова вероятность для студента получить зачет, если он знает решение 18 задач по дифференциальному и 15 по интегральному исчислению?
Решение. Пусть событие А означает, что студент получит зачет, т.е. решит предложенную ему задачу. Задача может быть по одной из двух тем, поэтому гипотезами будут следующие события: Н 1 – получена задача по дифференциальному исчислению; Н 2 – получена задача по интегральному исчислению.
Так как по условию задачи имеется 20 задач по дифференциальному и
30 задач по интегральному исчислению, то
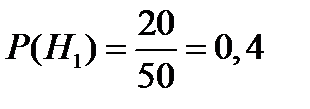и 
.
Событие А/Н 1 означает, что студент решит задачу, если эта задача по дифференциальному исчислению, следовательно, 
.
Событие А/Н 2 означает, что студент решит задачу, если эта задача по интегральному исчислению, следовательно, 
.
По формуле (10.15) получим 
. ■
Обратимся к примеру 14 и несколько изменим его условие.
Пример 16. В условиях примера 14, предположим, что шар вынут и известно, что он оказался белым, т.е. событие А произошло. Какова вероятность того, что шар был вынут из первого ящика?
Таким образом, требуется найти вероятность того, что шар был вынут из первого ящика, если он оказался белым, т.е. найти Р (Н 1/ А).
Необходимо различать две вероятности: Р (Н 1) и Р (Н 1/ А).
Р (Н 1) – вероятность того, что шар будет вынут из первого ящика, т.е вероятность события Н 1, вычисленная до испытания.
Р (Н 1/ А) – вероятность того, что шар был выбран из первого ящика, если он оказался белым, т.е. вероятность события Н 1, вычисленная при условии, что событие А уже произошло или, иначе, вероятность, вычисленная после опыта.
Аналогичные вероятности могут быть получены и для остальных гипотез Н 2 и Н 3 в примере и для Нi, i = 1, 2, …, n в общем случае.
Вероятности гипотез Р (Нi), i = 1, 2, …, n называются априорными вероятностями, т.е. «доопытными».
Условные вероятности гипотез Р (Нi/A), i = 1, 2, …, n называются апостериорными вероятностями, т.е. «послеопытными».
Итак, в результате решения подобного рода задач, известные до опыта априорные вероятности гипотез Р (Нi)подвергаются переоценке после того, как в результате испытания произошло событие А, т.е. происходит переход к апостериорным вероятностям гипотез Р (Нi/A).
Выведем общую формулу для условных вероятностей гипотез.
Пусть Н 1, Н 2, …, Нn – полная группа событий (гипотезы) для некоторого испытания. Событие А может произойти вместе с одним из событий полной группы, следовательно, 
. По теореме умножения вероятностей получим
, i = 1, 2, …, n.
Левые части последних равенств равны, следовательно, равны и их правые части, т.е. 
.
Отсюда, с учетом того, что , получаем
(16)
или, применяя к знаменателю формулу полной вероятности:
(17)
Формулы (10.16) и (10.17) называются формулами Байеса.
Формулы Байеса позволяют определить для любого события А, вероятность которого не равна нулю, условную вероятность Р (Нi/A), когда известно, что событие А уже произошло в результате испытания.
Имеет место формула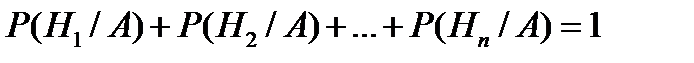 
, так как события, вероятности которых суммируются в левой части предлагаемой формулы, образуют полную группу событий для данного испытания.
Вернемся к примеру 10.16 и найдем вероятность того, что шар был вынут из первого ящика: 
. ■
Формулы Байеса находят широкое применение. Так, например, если решается какая-то экономическая задача с недостаточной информацией, то по мере расширения информации может быть проведена и корректировка найденного ранее решения.
