Вращательное движение −это движение,при котором все
точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. При вращательном движении скорости и ускорения различных точек тела неодинаковы. Поэтому в качестве общих кинематических характеристик движения тела при вращении вводятся угол поворота, угловая скорость и угловое ускорение тела. При вращении тела угол поворота изменяется со временем по некоторому закону ϕ = ϕ(t), который называется
уравнением вращательного движения тела.
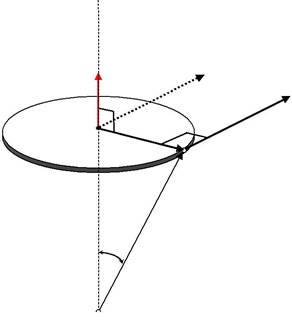
Угловой скоростью тела называется вектор,численно равныйпервой производной по времени от угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:
| r | ϕ | r | ||
| d ϕ | ||||
| ω= lim | t | = dt. | (1.6.1) |
Вектор угловой скорости направлен по оси вращения, причем так, чтобы вращение, рассматриваемое с конца вектора угловой скорости, происходило против хода часовой стрелки (рис 1.6.1).
| Единицей угловой скорости яв- | |||||
| ляется рад/с. | |||||
| r | r | Скорость | произвольной | ||
| υ | точки вращающегося тела назы- | ||||
| ω | υ | ||||
| вается линейной скоростью этой | |||||
| O | r r | точки. | |||
| При равномерном враще- | |||||
| нии угловая скорость не изменя- | |||||
| ется со временем, то есть явля- | |||||
| r 0 | ется постоянной величиной (ω = | ||||
| θ | = const). Тогда | ||||
| t 2 | − t 1)=ωΔ t. | ||||
| ϕ=ω ∫ d t =ω (t 2 | |||||
| O * | t 1 | ||||
| Рис. 1.6.1 | Равномерное | вращение |
характеризуется периодом вращения и частотой вращения.
Период вращения −это время,за которое точка совершает одинполный оборот, т. е. поворачивается на угол ϕ = 2π и на основании
выражения (1.6.1) T = 2ωπ.

Частота вращения −это число полных оборотов,котороеделает точка при равномерном вращении, за единицу времени:
n = T 1=2ωπ,откудаω= 2π n.


Для характеристики неравномерного вращения тела вводится понятие углового ускорения.
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
| ε = | d ω | = | d | d ϕ | = | d 2ϕ | . | (1.6.2) | |
| dt | dt | dt 2 | |||||||
| dt |
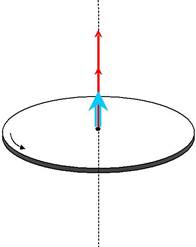
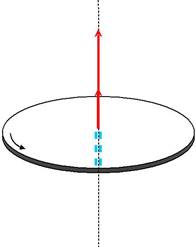
При ускоренном вращении вектор углового ускорения сонаправлен с вектором угловой скорости, а при замедленном − противоположен ему.
В случае равнопеременного движения точки по окружности (ε =
= const) угловая скорость определяется по формуле
| r | t | r | r r t | |||
| ω | r | r | ω | |||
| ∫ | d ω=∫ε dt | ⇒ ∫ | d ω= ε∫ dt | |||
| r | r | |||||
| ω0 | ω0 | |||||
| ω | ||||||
| ω0 | ||||||
| εr | ||||||
| O |
| ⇒ | r | r | ⇒ | r | r | |
| ω − ω0 | = ε t | ω = ω0 | + ε t. (1.6.3) |
ω0
ω
O 
 ε
ε
Рис. 1.6.2
Или в скалярном виде
| ω = ω0 ± ε t. | (1.6.4) |
Проинтегрировав выражение (1.6.1) можно получить формулу для угла поворота тела
| ϕ= ϕ | ±ω t ± | ε t 2 | . | (1.6.5) | ||
| Исключив из последнего уравнения t, получим | ||||||
| ±2εϕ= ω2 − ω2, | (1.6.6). | |||||
где ϕ = 2π N, N − число полное число оборотов, совершенных телом. В случае ε = ε(t), угловая скорость и закон вращательного дви-
жения определяются следующими формулами
| t | t | |
| ω=ω0 + ∫ ε(t) dt, | ϕ= ∫ ω(t) dt. | (1.6.7) |




