Магнетизм известен, по крайней мере, с V века до нашей эры. Некоторые камни, найденные вблизи города Магнезия (теперь Манисса) в Турции, обладали тем свойством, что, будучи свободно подвешеными на нити, они всегда ориентировались в определенном направлении. Куски такой магнитной руды использовались мореплавателями в качестве указателя направления. Китайцами был создан компас, т. е. свободно вращавшаяся магнитная стрелка. В 1600 году Гильберт, с целью объяснить магнетизм Земли, изготовил шар из магнитной руды и исследовал, каким образом шар действует на маленькую железную стрелку. Он обнаружил сходство поведения этой стрелки с поведением стрелки компаса вблизи Земли и пришел к заключению, что Земля представляет собой гигантский магнит.
В 1820 г. датский физик Х. Эрстед показывал студентам магнитное действие тока. При включении тока отклонилась стрелка случайно оказавшегося рядом компаса. Описание этого опыта вызвало лавину новых открытий. Дело в том, что хотя магнитные свойства веществ были известны давно, природа этих свойств была не ясна. После опыта Эрстеда Ампер выдвинул гипотезу о том, что свойства постоянных магнитов обусловлены циркулирующими в их толще постоянными круговыми токами (молекулярными токами). Эта гипотеза подтвердилась в дальнейшем в XX веке, когда выяснилось, что электроны вращаются вокруг ядра и это движение можно рассматривать как круговой ток.
Таким образом, магнетизм обусловлен движущимися зарядами. Движущиеся заряды (токи) изменяют свойства окружающего их пространства и создают в нем магнитное поле. Это поле проявляется в том, что на магнитную стрелку и на проводники с током действуют силы.
Так родилась новая область физики – электродинамика. Частью электродинамики (электромагнетизма) является магнитостатика, изучающая не изменяющиеся во времени (стационарные, или постоянные) магнитные поля.
Магнитное поле – силовое поле (подобно гравитационному или электрическому полю), окружающее токи и постоянные магниты. Магнитное поле не действует на неподвижные заряды, оно может создаваться только движущимися зарядами и действует только на движущиеся заряды. Магнитные силы, действующие со стороны магнитного поля на движущиеся заряды, могут:
– искривлять их траекторию (если заряд движется в свободном пространстве);
– отклонять проводник (если заряды движутся в проводнике);
– поворачивать контур (если проводник образует замкнутый контур).
Все объекты, на которые действует магнитное поле:
1. движущиеся заряды,
2. проводники с током,
3. контуры с током,
4. постоянные магниты,
5. изменяющееся электрическое поле,
являются источниками магнитного поля.
Открытие Эрстеда позволило качественно изменить эксперименты по изучению магнитных полей. Теперь вместо магнитов стали изучать взаимодействие проводов с током, и в том же 1820 г. были сформулированы законы Био–Савара‑Лапласа и Ампера.
Модуль силы взаимодействия бесконечно длинных параллельных проводников с током определяется законом Ампера (рис. 3.1):
, (3.1)
где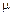 
– магнитная проницаемость среды; 
и 
– силы токов; 
–расстояние между проводниками;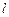 
– длина проводника.
Как видно из рис. 3.1, сонаправленные параллельные токи притягиваются, противоположно направленные – отталкиваются.
Рис. 3.1 Магнитное взаимодействие параллельных
и антипараллельных токов
Магнитная индукция
Для описания магнитного поля нужно ввести его характеристики. Казалось бы, это можно сделать так же, как, например, в электричестве, по силовому действию поля на пробный заряд. Но, как оказывается, магнитных зарядов в природе нет, поэтому в качестве объекта, на который действует сила со стороны магнитного поля, можно выбрать любой из объектов: движущийся заряд; проводник с током; контур с током; магнит.
Для обнаружения наличия и исследования характеристик магнитного поля чаще всего применяется замкнутый контур с током малых размеров. Если внести такой пробный контур в магнитное поле, он установится определенным образом, т. е. поле оказывает на контур ориентирующее действие. Это можно использовать для определения направления магнитного поля. Для этого надо условиться, как характеризовать ориентацию контура в пространстве. Направление нормали выбирается по правилу правого буравчика: за положительное направление нормали принимается направление поступательного движения буравчика, который вращается в направлении тока, текущего в рамке (рис. 3.2).
Рис. 3.2 Определение положительной нормали к контуру с током
За направление магнитного поля в месте расположения контура принимается то направление, вдоль которого располагается положительная нормаль контура.
Пробный контур можно использовать и для количественной оценки магнитного поля. Для этого вводится понятие магнитного момента контура с током
, (3.2)
где 
– единичная положительная нормаль к контуру, направление которой связано с направлением тока в контуре правилом правого винта.
Если рамка содержит 
витков провода, то магнитный момент рамки
. (3.3)
Из эксперимента известно, что если контур с током повернуть так, чтобы направление нормали и поля не совпадали, возникает вращающий момент, стремящийся вернуть контур в равновесное положение. Рамка с током будет поворачиваться в магнитном поле до тех пор, пока вращающий момент не станет равным нулю. В этом случае магнитный момент будет направлен по магнитному полю. Следовательно, магнитное поле поворачивает магнитные моменты так, чтобы они были направлены по полю.
Можно показать, что вращающий момент 
, действующий на контур с током в магнитном поле,
, (3.4)
, (3.5)
где 
‑ вектор магнитной индукции.
Вращающий момент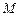 
зависит как от свойств поля, т. е. магнитной индукции в данной точке , так и от свойств самого контура 
.
Если в одну и ту же точку поля помещать контуры с разными характеристиками, т. е. с разными , но одинаково ориентированные, т. е. 
, то на них будут действовать разные по величине вращающие моменты. Однако отношение 
будет для всех контуров одно и тоже и может быть принято для количественной характеристики поля. Именно этот факт, позволяет определить модуль вектора магнитной индукции
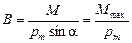, (3.6)
где 
‑ максимальный вращаюший момент, действующий на рамку с током.
Вектор магнитной индукции – вектор, направление которого определяется направлением положительной нормали к пробному контуру с током. В СИ единицей измерения магнитной индукции принят 1 Тесла – Тл.
Определение магнитной индукции, полученное из формулы (3.6) не является единственно возможным. Ниже будет показвно, что модуль можно определить, например, следующим образом:
,
где 
– максимальная сила, действующая на точечный заряд 
, движущийся со скоростью 
.
Уравнения (3.4) ‑ (3.6) были получены в предположении, что поле однородно в пределах площади пробного контура с током, т. е.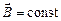 
. Если же это не выполняется, то следует рассматривать силу, действующую на контур с током в неоднородном магнитном поле, в виде
,
где производная берется по направлению нормали 
или по направлению вектора . Направление вектора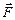 
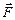в общем случае не совпадает ни с вектором , ни с вектором . Вектор совпадает по направлению лишь с направлением элементарного приращения вектора , взятого в направлении .
Как и в случае электрического поля, можно ввести для наглядности линии индукции магнитного поля. Линии магнитной индукции – это линии, касательные к которым в каждой точке совпадают с направлением вектора магнитной индукции в этой точке (рис. 3.3).
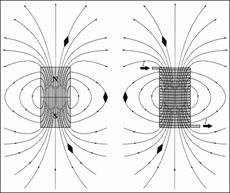
Рис. 3.3 Линии магнитной индукции полей постоянного магнита
и катушки с током
Поскольку магнитная индукция является силовой характеристикой магнитного поля, для нее справедлив принцип суперпозиции. Если магнитное поле создается несколькими источниками, то вектор магнитной индукции в данной точке определяется как сумма векторов магнитной индукции полей, создаваемых каждым источником в отдельности:
; 
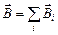, (3.7)
где 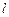– длина проводника с током, создающим магнитное поле.
Помимо макроскопических токов, текущих в проводниках, в любом теле существуют микроскопические токи, создаваемые движением электронов в атомах и молекулах («молекулярные» токи Ампера). Эти микроскопические токи создают свое магнитное поле и могут поворачиваться в магнитных полях внешних токов. Если возле какого-либо тела поместить проводник с током (макроток), создающий вокруг себя магнитное поле, то под действием этого поля микроскопические токи во всех атомах будут определенным образом поворачиваться и создадут в теле дополнительное поле. Таким образом, вектор магнитной индукции характеризует результирующее магнитное поле, создаваемое всеми микро- и макро- токами. При одном и том же токе 
в проводнике величина вектора в различных средах будет иметь разные значения.
Для характеристики магнитного поля, создаваемого самим макротоком вводится вспомогательное понятие вектора напряженности магнитного поля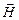 
, не зависящего от свойств среды. Связь между индукцией и напряженностью магнитного поля (в изотропной среде, в слабых полях) дается выражением:
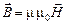, (3.8)
где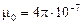 
, Гн/м ‑ магнитная постоянная; m ‑ магнитная проницаемость среды (для вакуума 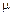=1). Магнитная проницаемость среды m показывает во сколько раз магнитное поле макроскопических токов усилено за счет поля микроскопических токов среды.
Во многих случаях напряженость позволяет значительно упростить изучение магнитного поля в магнетиках
, (3.9)
где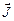 
– намагниченность вещества.
Закон Био-Савара-Лапласа
После опытов Эрстеда началось интенсивное изучение магнитного поля постоянного электрического тока. В 1820 году французские ученые Био и Савар исследовали магнитные поля, создаваемые в воздухе прямолинейным током, круговым током, катушкой с током и т. д. На основании многочисленных опытов они пришли к следующим выводам:
1. во всех случаях индукция магнитного поля зависит прямо пропорционально от силы тока ;
2. магнитная индукция зависит от формы и размеров проводника;
3. магнитная индукция в произвольной точке поля зависит от расположения этой точки по отношению к проводнику с током.
Французский ученый Лаплас проанализировал экспериментальные данные, полученные Био и Саваром. Он учел векторный характер характеристик магнитного поля и высказал гипотезу о том, что магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока.
Закон Био–Савара–Лапласа позволяет рассчитать индукцию магнитного поля, создаваемого проводником с током, в любой точке пространства (рис. 3.4):
; 
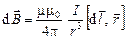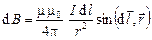, (3.10)
где – сила тока; 
– элемент длины провода (вектор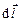 
совпадает по направлению с током ); 
– радиус-вектор, проведенный от элемента к точке наблюдения.
Рис. 3.4 Закон Био-Савара-Лапласа
Как следует из формулы (3.10) вектор 
направлен перпендикулярно к плоскости, проходящей через 
и точку, в которой вычисляется поле, причем так, что вектора , , связаны правилом правого винта (буравчика).
В соответствии с принципом суперпозиции результирующую магнитную индукцию поля проводника с током конечных размеров и произвольной формы можно найти по формуле
. (3.11)
