Электростатических полей. Поле диполя

 

Рассмотрим метод определения значения и направления вектора напряженности 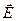в каждой точке электростатического поля, создаваемого системой неподвиж­ных зарядов Q ₁, Q ₂, … Q _n.

Результирующая сила F, действующая со стороны поля на пробный заряд Q_o, равна векторной сумме сил F _n приложенных к нему со стороны каждого из зарядов Q_i:

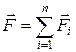(4.1)

Так как 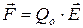и 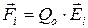, где Е – напряженность результирующего по­ля, а Е, – напряженность поля, создавае­мого зарядом Q_i. Подставляя последние выражения в (4.1), получим

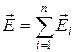(4.2)

Формула (4.2) выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создавае­мого системой зарядов, равна геометриче­ской сумме напряжённостей полей, со­здаваемых в данной точке каждым из зарядов в отдельности.

Принцип суперпозиции применим для расчета электростатического поля электрического диполя. Электрический диполь – система двух равных по модулю разноимённых точечных зарядов (+ Q, – Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя l. Вектор

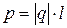(4.3)

совпадающий по направлению с плечом диполя и равный произведению заряда ½ q ½ на плечо l, называется электрическим моментом диполя р или дипольным моментом (рис. 4.1).

 

Согласно принципу суперпозиции, напряженность Е поля диполя в произвольной точке

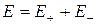
где Е ₊ и Е _- – напряженности полей, создаваемых соответственно положительным и отрицательным зарядами. Воспользовавшись этой формулой, рассчитаем на­пряженность поля на продолжении оси диполя и на перпендикуляре к середине его оси.

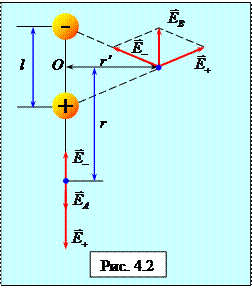1. Напряженность поля на продолже­нии оси диполя в точке А (рис. 4.2).

Как видно из рисунка, напряженность поля диполя в точке А направлена по оси диполя и по модулю равна

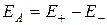
Обозначив расстояние от точки А до середины оси диполя через r, на основании формулы 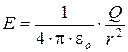для вакуума можно записать

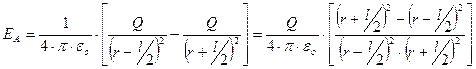
Согласно определению диполя, 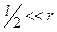, поэтому

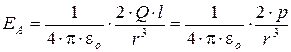
2. Напряженность поля на перпенди­куляре, восставленном к оси из его середи­ны, в точке В (рис. 4.2).

Точка В равноудалена от зарядов, поэтому

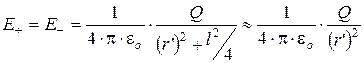(4.4)

где r’ – расстояние от точки В до середины плеча диполя.

Из подобия равнобедренных треугольников, опирающихся на плечо диполя и вектор Е _B, получим

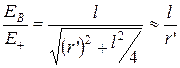
откуда

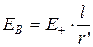(4.5)

Подставив в выражение (4.5) значение (4.4), получим

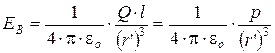
Вектор Е _в имеет направление, противоположное электрическому моменту диполя (вектор p направлен от отрицательного заряда к положительному).

 

В качестве примера применения принципа суперпозиции полей на рис. 3.2. изображена картина силовых линий поля электрического диполя – системы из двух одинаковых по модулю зарядов разного знака q и –q, расположенных на некотором расстоянии l.

 

 

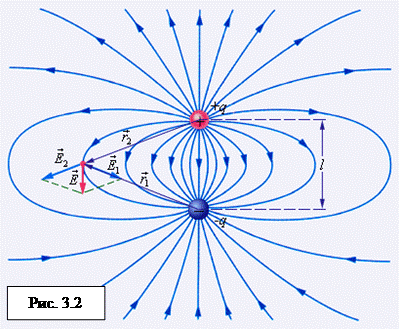Силовые линии поля электрического диполя .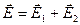

 

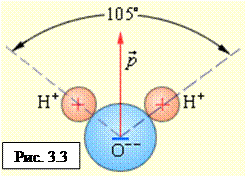
Электрическим дипольным моментом обладает, например, нейтральная молекула воды (H₂O), так как центры двух атомов водорода располагаются не на одной прямой с центром атома кислорода, а под углом 105° (рис. 3.3). Дипольный момент молекулы воды p = 6,2·10^–30 Кл · м.

 

§5. Теорема Гаусса