Однородный (пассивный) участок электрической цепи. Участокэлектрической цепи, не содержащий источников электроэнергии, называ-ется однородным (рис. 5.2.1). Для такого участка (проводника) закон Ома, который установлен экспериментально, гласит: сила тока I в проводнике прямо пропорциональна напряжению U на его концах и обратно пропор-циональна электрическому сопротивлению R проводника (участка):
| I | U. | (5.2.1) | |||
| R | |||||
| R | I | ||||
| 1 | 2 | ||||
| U =1–2 | |||||

Рис. 5.2.1
Единица сопротивления – ом (1 Ом = 1 В/А).
Выражение (5.2.1) является законом Ома для однородного участ-ка цепи в интегральной форме.
Величина g, обратная сопротивлению, называется электрической проводимостью (или электропроводностью)проводника:
| g | . | (5.2.2) | ||
| R |
Единица электропроводности – сименс (1 Cм = 1 А/В = 1/Ом). Сопротивление и электропроводность проводника являются его характеристиками, которые зависят от природы вещества проводника, его геометрии и состояния. Для однородного линейного проводника сопротивление прямо пропорционально его длине l и обратно пропор-
ционально площади поперечного сечения S проводника:
| R | l | , | (5.2.3) | |
| S | ||||
где – удельное сопротивление вещества.
Единица удельного сопротивления – ом-метр (1 Ом · м).
Величина 1 называется удельной электрической проводимо-
стью (или удельной электропроводностью)материала проводника.
Единица удельной электропроводности сименс на метр (1 См/м = = 1 Ом–1 · м–1).
Опытным путем установлено, что для большинства металлов с повышением температуры удельное сопротивление (а значит, и со-противление) увеличивается. Такое изменение удельного сопротивле-ния (сопротивления) описывается линейным законом, если интервал изменения температуры достаточно мал:
| = 0(1 + t), или R = R 0(1 + t), | (5.2.4) |
где и 0, R и R 0 – соответственно удельные сопротивления и сопро-тивления проводника при температурах t °С и 0°С; – температурный коэффициент сопротивления.
Для всех химически чистых металлов коэффициент близок к 1/273.
Зависимость сопротивления металлов от температуры исполь-зуют в различных измерительных и автоматических устройствах (например, термисторы, термометры сопротивления), а зависи-мость удельного сопротивления металлов от механических воздей-ствий, которая для чистых металлов и сплавов возрастает при рас-тяжении, используется для измерения деформаций и механических напряжений.
2 I
E
1 

 E
E
| S | l | |
Рис. 5.2.2
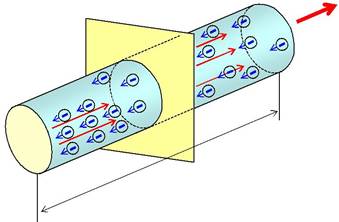
Расчет силы тока в проводящей среде в общем случае осуществля-ется на основе закона Ома в дифференциальной форме. Для его вывода рассмотрим небольшой отрезок трубки тока (рис. 5.2.2) в однородной и изотропной проводящей среде. На рисунке l – расстояние между точками 1 и 2, потенциалы которых соответственно равны 1 и 2, а S –средняя величина площади сечения трубки тока.
| По закону Ома I | U | 2, где R | l | |||||||||||||
| 1 | . | |||||||||||||||
| R 12 | R 12 | S | ||||||||||||||
| Далее учтем, что I = jS и 1. | ||||||||||||||||
| Тогда | ||||||||||||||||
| jS | l S | j | l . | |||||||||||||
| Но lim | d | E,где Е –напряженность электрического | ||||||||||||||
| dl | ||||||||||||||||
| l 0 | l |
поля в некоторой точке внутри проводника. Таким образом, имеем:
| j = E,или | (5.2.5) | ||||
| j | E | 1 E. | |||
Плотность электрического тока в любой точке проводящей среды вычисляется как произведение удельной электропроводности среды на напряженность электрического поля в этой точке.
Выражение (5.2.5) является з аконом Ома для однородного участ-ка цепи в дифференциальной форме.
Сравнив формулу (5.2.5) с уравнением (5.1.7), можем сказать, что средняя скорость упорядоченного движения (скорость дрейфа) носи-телей заряда пропорциональна напряженности поля, т. е.
| aE. | (5.2.6) | ||
| u |


где a – подвижность носителей заряда. Подставив выражение (5.2.6)
| в уравнение (5.1.7), получим: | ||
| (5.2.7) | ||
| j enaE E. |
Таким образом, удельная электропроводимость среды определя-ется концентрацией носителей заряда и их подвижностью, т. е. = ena.
Неоднородный (активный) участок электрической цепи. Если впроводнике создать электрическое поле и не принять мер для его под-держания, то перемещение носителей тока приведет к тому, что потен-
циалы всех точек цепи выравняются, и поле внутри проводника исчез-нет, а ток прекратится. Для того чтобы поддерживать ток достаточно длительное время, нужно от конца проводника с меньшим потенциалом непрерывно отводить приносимые сюда заряды, а к концу с большим потенциалом непрерывно их подводить (разделение разноименных за-рядов), т. е. необходимо наличие в цепи устройства, способного созда-вать и поддерживать разность потенциалов. Устройство, способное соз-давать и поддерживать разность потенциалов, называют источником электрической энергии (или генератором).В источниках электроэнер-
гии на носители зарядов действуют силы неэлектростатического проис-хождения, которые называются сторонними силами. Они могут быть обусловлены химическими процессами, вихревыми электрическими по-лями, диффузией носителей заряда в неоднородной среде и т. д.
Количественной характеристикой сторонних сил является напря-женность E ст, которая определяется сторонней силой, действующей на
единичный положительный заряд. Сторонние силы можно охарактери-зовать работой, которую они совершают над перемещающимися по цепи зарядами. Физическая величина, равная работе сторонних сил по пере-мещению единичного положительного заряда в цепи или на ее участке, называется электродвижущей силой (ЭДС) источника электроэнергии:
| A ст | . | (5.2.8) | ||
| q |
Эта работа совершается за счет энергии, затрачиваемой в источ-нике тока.
Работа сторонних сил по перемещению заряда q 0 на участке цепи равна:
| A ст F ст dl | q пр E ст dl. | (5.2.9) | |||
Отсюда ЭДС, действующая в замкнутой цепи, – это циркуляция вектора напряженности поля сторонних сил:
| E ст dl. | (5.2.10) |
Для поля сторонних сил циркуляция его напряженности по замкнутому контуру не равна нулю. Поэтому поле сторонних сил не-потенциально.
Участок электрической цепи называется неоднородным, если он со-держит источник (или источники) электрической энергии (рис. 5.2.3).
| R | I | r, | |||||||
| 1 | 2 | ||||||||
| U = (1–2) + | |||||||||

Рис. 5.2.3
Рассмотрим участок цепи, полное сопротивление которого R 12 и 1 > 2. Для любой точки данного участка напряженность результи-
рующего поля E E эл E ст. Поэтому з акон Ома для неоднородного участка цепи в дифференциальной форме запишется в виде:
| jE эл E ст. | (5.2.11) |
В случае если на заряд кроме сторонних сил действуют силы электростатического поля, то результирующая сила, действующая в каждой точке цепи на заряд, равна:
| F | F эл F ст q пр E эл E ст. | (5.2.12) |
Тогда работа, совершаемая этой силой на участке цепи 1 → 2, оп-ределяется выражением
| A | q | . | (5.2.13) | |||||||||||
| q | E | эл | dl | q | E | dl | ||||||||
| пр | пр | ст | пр | |||||||||||
Величина, численно равная работе, совершаемой электрическими и сторонними силами при перемещении единичного положительного заряда, называется падением напряжения, или просто напряжением на данном участке цепи:
| U | A 12 | . | (5.2.14) | |||||
| q пр | ||||||||
| Так как U 12 = IR 12, то | ||||||||
| IR 12=1–2+12. | (5.2.15) |
С учетом выражения (5.2.15) закон Ома для неоднородного уча-стка цепи в интегральной форме принимает вид:
| I | 2 | 2 | (5.2.16) | ||||||||
| 1 | 12 | 1 | , | ||||||||
| R 12 | R r | ||||||||||
где R – сопротивление внешнего участка цепи; r – внутреннее сопро-тивление источника тока.
При использовании (5.2.16) для расчета характеристик участка электрической цепи пользуются правилами знаков для силы тока и ЭДС: если направление тока (выбранное произвольно) совпадает с на-правлением движения по участку от точки 1 до точки 2, то сила тока I берется со знаком «плюс», в противоположном случае сила тока I бе-рется со знаком «минус»; если внутри источника ток идет от катода к аноду, т. е. напряженность поля сторонних сил в источнике совпадает по направлению с током на участке цепи, то ЭДС этого источника считается положительной, в противоположном случае ЭДС этого ис-точника считается отрицательной.
| I 1 | 1, r 1 | R 1 | |||||||
| 1 | 2 | ||||||||
I 2
R 2 2, r 2
Рис. 5.2.4
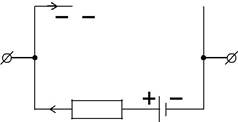
Для электрической цепи, состоящей из двух участков и изобра-женной на рис. 5.2.4, согласно выбранному направлению движения по каждому участку от точки 1 до точки 2 и правилам знаков уравнения, записанные с применением закона Ома (5.2.16) для неоднородного участка цепи, имеют следующий вид:
| I | I | ||||||||||
| ; | . | ||||||||||
| R 1 | r 1 | R 2 | r 2 | ||||||||
Если цепь замкнута, то в выражении (5.2.16) 1 – 2 = 0, и получа-
ем выражение закона Ома для замкнутой цепи (рис. 5.2.5):
| I | ||||||
| . | (5.2.17) | |||||
| R | R r | |||||
Если R << r, то происходит короткое замыкание источника энер-гии. Сила тока короткого замыкания достигает максимального значе-ния и равна:
| I max | I к.з. | (5.2.18) | |||||||||
| r | |||||||||||
| , | r | ||||||||||
| I | |||||||||||
| R | |||||||||||

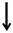

Рис. 5.2.5
Для большинства реальных источников из-за малости r режим ко-роткого замыкания является аварийным, и поэтому применяют защиту от короткого замыкания.






