Пусть система состоит из 
точек и, следовательно, ее положение в пространстве в каждый момент времени определяется 
координатами точек системы, например декартовыми 
.
Предположим, что на систему наложены голономные связи, уравнения которых в общем случае могут содержать и производные от координат точек, но после их интегрирования они свелись к геометрическим и имеют форму
, 
. (222)
Освобождающие связи, выражающиеся неравенствами, не рассматриваются. Таким образом, координат связаны 
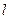уравнениями и независимых координат будет 
.
Любые 
декартовых координат можно задать независимо друг от друга. Остальные координаты определятся из уравнений связей. Вместо независимых декартовых координат можно выбрать любые другие независимые параметры 
, зависящие от всех или части декартовых координат точек системы. Эти независимые параметры, определяющие положение системы в пространстве, называются обобщенными координатами системы. В общем случае они могут зависеть от всех декартовых координат точек системы, т. е.
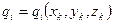, (223)
где 
изменяется от 1 до . Задание обобщенных координат полностью определяет положение точек системы относительно выбранной системы отсчета, например декартовых осей координат.
У свободной точки три обобщенные координаты. Если точка должна двигаться по заданной поверхности, то обобщенных координат только две и т.д. Используя уравнения связей (222) и выражения обобщенных координат через декартовы (223), можно выразить декартовы координаты через обобщенные, т.е. получить
,
,
.
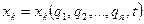Соответственно, для радиуса-вектора каждой точки системы 
, получим
. (224)
В случае стационарных связей время явно не входит в уравнения связей. Для голономных систем вектор возможного перемещения точки 
в соответствии с (224) можно выразить в форме
. (225)
Система, имеющая независимых обобщенных координат, характеризуется также независимыми возможными перемещениями или вариациями 
, если связи голономны. Для голономных систем число независимых возможных перемещений совпадает с числом независимых обобщенных координат. Следовательно, число степеней свободы голономной системы равно числу независимых обобщенных координат этой системы, т. е. . Для неголономных систем в уравнения связей могут входить производные от декартовых координат точек и даже могут быть такие уравнения связей, в которые входят только одни производные. Такие уравнения связей наложат ограничения на вариации , и, следовательно, уменьшат число независимых вариаций, не связывая функциональной зависимостью сами обобщенные координаты . Число степеней свободы неголономной системы, равное числу независимых возможных перемещений, меньше числа обобщенных координат системы. В дальнейшем рассматриваются только голономные системы, т. е. системы с голономными связями.
Обобщенные силы
Запишем сумму элементарных работ сил, действующих на точки системы, на возможном перемещении системы:
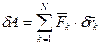. (226)
Пусть голономная система имеет степеней свободы и, следовательно, ее положение в пространстве определяется 
обобщенными координатами .
Подставляя (225) в (226) и изменяя порядок суммирования по индексам и 
, получим
. (226')
где скалярная величина
называется обобщенной силой, отнесенной к обобщенной координате 
. Используя известное выражение для скалярного произведения двух векторов, сообщенную силу можно также представить в виде
, (227)
– проекции силы на оси координат; – координаты точки приложения силы.
Размерность обобщенной силы в соответствии с (226') следующим образом зависит от размерности 
, совпадающей с размерностью 
:
, (228)
т. е. размерность обобщенной силы равна размерности работы силы (энергии) или момента силы, деленной на размерность обобщенной координаты, к которой отнесена обобщенная сила. Из этого следует, что обобщенная сила может иметь размерность силы или момента силы.
