Пусть механическая система совершает движение относительно основной системы координат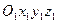 
. Возьмем подвижную систему координат 
с началом в центре масс системы 
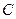, движущуюся поступательно относительно основной системы координат. Можно доказать справедливость формулы:
, (177)
где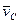 
– абсолютная скорость центра масс, 
.
Величина 
является кинетическим моментом системы относительно центра масс для относительного движения относительно системы координат, движущейся поступательно вместе с центром масс, т. е. системы .
Формула (176) показывает, что кинетический момент абсолютного движения системы относительно неподвижной точки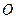 
равен векторной сумме кинетического момента центра масс относительно той же точки, если бы в центре масс была сосредоточена вся масса системы, и кинетического момента системы относительно центра масс для относительного движение системы по отношению к подвижной системе координат, движущейся поступательно вместе с центром масс.
Теорема об изменении кинетического момента системы относительно центра масс для относительного движения системы по отношению к системе координат, движущейся поступательно с центром масс; она формулируется так же, как если бы центр масс был неподвижной точкой:
или 
, (178)
где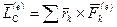 
является главным моментом всех внешних сил относительно центра масс.
Дифференциальные уравнения плоского движения твердого тела
Для твердого тела, совершающего плоское движение и, следовательно, имеющего три степени свободы, соответственно получим следующие три дифференциальных уравнения:
, 
, 
. (179)
С помощью этих уравнений можно решать две основные задачи: по заданному плоскому движению твердого тела находить действующие на тело внешние силы и по заданным внешним силам и начальным условиям определять его движение. При решении этих задач должны быть заданы масса тела и его момент инерции.
Теорема об изменении кинетической энергии
Работа силы
Работа силы на каком-либо перемещении является одной из основных характеристик, оценивающих действие силы на этом перемещении.
Элементарная работа силы. Элементарная работа 
силы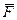 
на элементарном (бесконечно малом) перемещении 
определяется следующим образом (рис. 54):
, (180)
где 
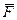– проекция силы на направление скорости точки приложения силы или на направление элементарного перемещения, которое считается направленным по скорости точки.
Элементарную работу можно представить, в виде:
, (181)
элементарная работа силы равна произведению элементарного перемещения ни проекцию силы на это перемещение. Отметим частые случаи, которые можно получить из (180):
, 
;
, 
;
, 
.
Таким образом, если сила перпендикулярна элементарному перемещению, то ее элементарная работа равна нулю. В частности, работа нормальной составляющей к скорости силы всегда равна нулю.
Приведем другие формулы для вычисления элементарной работы силы:
, (182)
элементарная работа силы равна скалярному произведению силы на дифференциал радиуса-вектора точки приложения силы.
, (183)
элементарная работа равна скалярному произведению элементарного импульса силы на скорость точки.
Аналитическое выражение элементарной работы:
. (184)
Полная работа силы. Полная работа силы 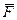на перемещении от точки 
до точки 
равна:
, (185)
Используя другие выражения для элементарной работы, полную работу силы можно представить также в виде
, (186)
или
, (187)
где момент времени 
соответствует точке , а момент времени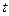 
– точке .
Из определения элементарной и полной работы следует:
1) работа равнодействующей силы на каком-либо перемещении равна алгебраической сумме работ составляющих сил на том же перемещении;
2) работа силы на полном перемещении равна сумме работ этой же силы на составляющих перемещениях, на которые любым образом разбито все перемещение.
Мощность. Мощность силы или работоспособность какого-либо источника силы часто оценивают той работой, которую он может совершить за единицу времени:
.
Учитывая определение для элементарной работы, мощность можно представить в виде
.
Таким образом, мощность равна скалярному произведению силы на скорость точки.
