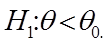Проверку статистической гипотезы осуществляют на основании данных выборки.Для этого используют специально подобранную СВ (статистику, критерий), точное или приближенное значение которой известно. Эту величину обозначают:
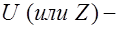если она имеет стандартизированное нормальное распределение;
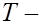если она распределена по закону Стьюдента;
χ2 - если она распределена по закону χ2;
если она имеет распределение Фишера.
В целях общности будем обозначать такую СВ через 
Таким образом, статистическим критерием или статистическим тестом называют СВ 
которая служит для проверки нулевой гипотезы. После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества:
- одно из них содержит значения критерия, при которых нулевая гипотеза отклоняется;
- другое – при которых она не отклоняется.
Совокупность значений критерия, при которых нулевую гипотезу отклоняют, называют критической областью.
Совокупность значений критерия, при которых нулевую гипотезу не отклоняют, называют областью принятия гипотезы.
Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия 
(вычисленное по выборке) принадлежит критической области, то нулевую гипотезу отклоняют. Если же наблюдаемое значение критерия принадлежит области принятия гипотезы, то нулевую гипотезу не отклоняют (принимают).
Точки, разделяющие критическую область и область принятия гипотезы, называют критическими.
В основу определения критических точек и критической области положен принцип практической невозможности маловероятных событий.
Пусть для проверки нулевой гипотезы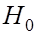 
служит критерий Предположим, что плотность распределения вероятности СВ в случае справедливости 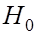имеет вид 
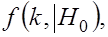а математическое ожидание равно 
Тогда вероятность того, что СВ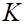 
попадет в произвольный интервал 
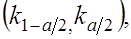можно найти по формуле:
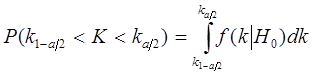(35)
Зададим эту вероятность равной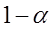 
и вычислим критические точки (квантили) 
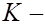распределения 
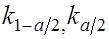из условий:
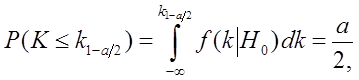(36)
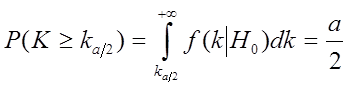(37)
Следовательно,
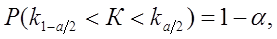
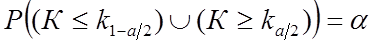(38)
Зададим вероятность 
настолько малой (0,05; 0,01), что попадание СВ за пределы интервала 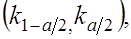можно было бы считать маловероятным событием. Тогда, исходя из принципа практической невозможности маловероятных событий, можно считать, что если 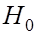справедлива, то при ее проверке с помощью критерия 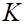по данным одной выборки наблюдаемое значение должно наверняка попасть в интервал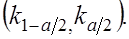 
Если же наблюдаемое значение попадает за пределы указанного интервала, то произойдет маловероятное, практически невозможное событие. Это дает основание считать, что с вероятностью 
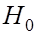нулевая гипотеза несправедлива.
Точки 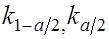называются критическими.
Критическая область 
называется двусторонней критической областью. Она определяется в случае, когда альтернативная гипотеза имеет вид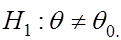 
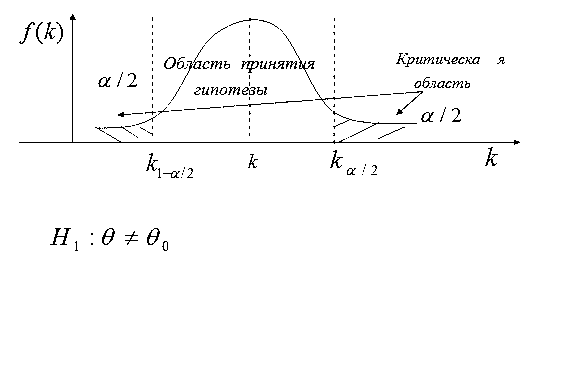
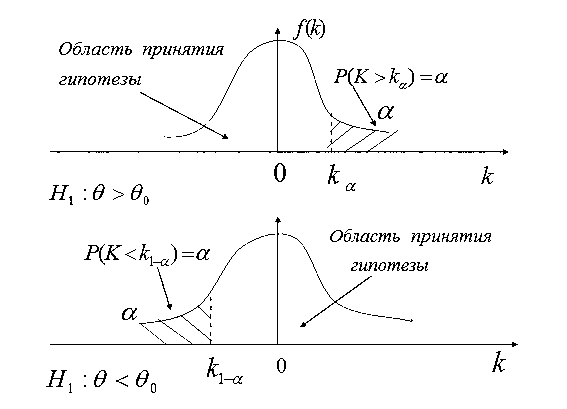
Кроме двусторонней, рассматривают также односторонние критические области – правостороннюю и левостороннюю.
Правосторонней называют критическую область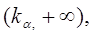 
определяющуюся из соотношения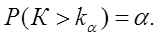 
Она используется в случае, когда альтернативная гипотеза имеет вид: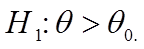 
Левосторонней называют критическую область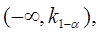 
определяющую из соотношения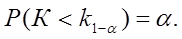 
Она используется в случае, когда альтернативная гипотеза имеет вид 
