Многие экономические показатели определяются несколькими числами, являясь многомерными СВ. Упорядоченный набор Х=(Х1, Х2, …, Хn) случайных величин называется многомерной (n-мерной) случайной величиной (или системой случайных величин, n-мерным вектором). Например, издержки предприятия включают в себя фиксированную и переменную составляющие; уровень жизни населения подразумевает использование большого числа показателей: ВНП на душу населения, распределение доходов, наличие товаров пи услуг, продолжительность жизни и т.д.
При проведении эконометрического анализа одно из главных мест занимает исследование взаимных связей СВ, при которых реализация одной из СВ влияет на вероятность определенной реализации других СВ.
Для описания n-мерной случайной величины используются следующие понятия:
1. Совместная вероятность
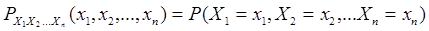 (39)
(39)
2. Совместная функция распределения
 (40)
(40)
3. Совместная плотность вероятностей
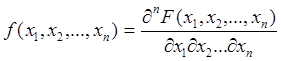 (41)
(41)
В двумерном случае для случайной величины (Х,Y) двумерная вероятность, функция распределения и плотность вероятностей будут определяться:
Р(Х=х, Y=y); F(x,y)=P(X<x, Y<y);  (42)
(42)
Свойства функции распределения F(x,y) и плотности вероятности двумерной случайной величины f(x,y) аналогичны свойствам одномерной случайной величины соответственно.
Если необходимо вычислить значения вышеуказанных функций при фиксированных величинах одной или нескольких случайных величин, то эти функции суммируются (усредняются) по лишним переменным. В результате получаются маргинальные (предельные) вероятности, функции распределения и плотности вероятности или условия согласованности:
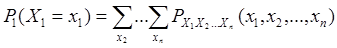 (43)
(43)
 (44)
(44)
 (45)
(45)
Для многомерных случайных величин кроме совместной вероятности (плотности вероятностей) определяются условные вероятности (условные плотности вероятностей).
Условным законом распределения одной из одномерных составляющих двумерной случайной величины (X,Y) называется ее закон распределения, вычисленный при условии, что другая составляющая приняла определенное значение (или попала в какой-то интервал).
Условная вероятность и условная плотность вероятностей случайной величины Х для двумерной случайной величины (X,Y) при условии, что случайная величина Y примет значение y (Y=y) определяются по формулам:
 ;
; 
В соответствии с условной вероятностью (условной плотностью вероятности) двух случайных величин можно определить совместную вероятность (совместную плотность вероятности) этих случайных величин:
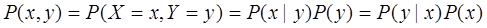 (46)
(46)
 (47)
(47)
Для независимых случайных величин X и Y выполняются следующие соотношения:
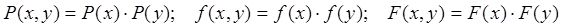 (48)
(48)
Построение закона распределения многомерной случайной величины является трудоемким процессом. Поэтому обычно для анализа степени взаимной связи СВ используют следующие числовые характеристики:
- смешанные моменты распределения;
- ковариацию;
- коэффициент корреляции.
Смешанным моментом порядка  называется величина:
называется величина:
 (49)
(49)
Например, 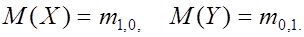
Центральным моментом порядка  называется величина:
называется величина:
 (50)
(50)
Например, 
Для описания связи между СВX и Y применяют центральный момент порядка 1,1  , который называется ковариацией СВ X и Y (или корреляционным моментом):
, который называется ковариацией СВ X и Y (или корреляционным моментом):
 (51)
(51)
Ковариация является абсолютной (зависящей от размерностей) мерой взаимосвязи (со-vary – «совместное изменение») переменных.
 (52)
(52)
Свойства ковариации:
1. 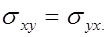
2. 
3. Если 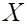 и
и  независимые СВ, то
независимые СВ, то 
4. 
5. 
Однако существенным недостатком ковариации является ее зависимость от размерностей рассматриваемых СВ. Поэтому при различных единицах измерения СВ одна и та же зависимость может выражаться различными значениями ковариаций. Кроме того, ковариация не позволяет определить силы (строгости) зависимости между рассматриваемыми СВ.
Для устранения данных недостатков вводится относительная мера взаимосвязи (безразмерная величина) – коэффициент корреляции.
Коэффициентом корреляции СВ 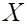 и
и  называют величину
называют величину
 (53)
(53)
Зависимость между СВ 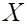 и
и  , характеризуемая коэффициентом корреляции, называется корреляцией.
, характеризуемая коэффициентом корреляции, называется корреляцией.
СВ 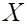 и
и  называется некоррелированными, если
называется некоррелированными, если  что равносильно равенству
что равносильно равенству  Если же
Если же 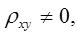 то СВ
то СВ 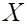 и
и  называют коррелированными.
называют коррелированными.
Свойства коэффициента корреляции:
1. 
2. 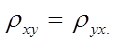
3. 
4. Если СВ 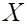 и
и  независимы, то
независимы, то 
5. 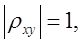 тогда, когда
тогда, когда  (т.е. между СВ
(т.е. между СВ 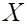 и
и  существует линейная функциональная зависимость).
существует линейная функциональная зависимость).
Заметим, что если 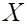 и
и  независимые СВ, то
независимые СВ, то 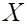 и
и 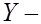 некоррелированные СВ. Обратное утверждение неверно.
некоррелированные СВ. Обратное утверждение неверно.
Ранее мы привели основные свойства и формулы расчета дисперсии, в частности дисперсии суммы двух независимых СВ (см. формулу 35).
В случае, когда СВ не являются независимыми, а коррелируют друга, формулы расчета дисперсии их суммы, либо разности имеют вид:
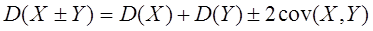 (54)
(54)
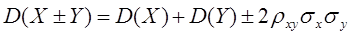 (55)
(55)
При независимости случайных величин последние слагаемые в этих формулах обращаются в ноль.
Выборочное наблюдение.
Генеральной совокупностью называется множество всех возможных значений или реализаций исследуемой СВ Х при данном реальном комплексе условий.
Выборкой (выборочной совокупностью) называют часть генеральной совокупности, отобранную для изучения.
Число элементов рассматриваемой совокупности называется ее объемом.
Изучение всей генеральной совокупности во многих случаях либо невозможно, либо нецелесообразно в силу больших материальных затрат.
Задачей статистического описания выборки является получение такого ее представления, которое позволит наглядно выявить вероятностные характеристики. Для этого применяются различные формы упорядочения данных в выборке – по возрастанию, по совпадающим значениям, по интервалам и т.п.
При анализе какого-то конкретного показателя 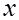 в фиксированный момент времени (либо без учета фактора времени) наблюдаемые значения
в фиксированный момент времени (либо без учета фактора времени) наблюдаемые значения  обычно упорядочивают по неубыванию:
обычно упорядочивают по неубыванию: 
Разность между максимальными и минимальными значениями СВ 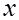 называется размахом выборки.
называется размахом выборки.
Пусть количество различных значений в выборке равно  Значение
Значение  называется вариантами.
называется вариантами.
Если значение  встретилось в выборке
встретилось в выборке 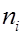 раз, то число
раз, то число 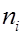 называется частотой значения
называется частотой значения  , а величина
, а величина 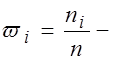 относительной частотой значения
относительной частотой значения  . Тогда наблюдаемые значения можно сгруппировать в статистический ряд:
. Тогда наблюдаемые значения можно сгруппировать в статистический ряд:
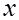
| 
| 
|
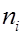
| 
| |

| 
|
По статистическому ряду можно построить эмпирическую функцию распределения 
 (1)
(1)
где  число значений случайной величины
число значений случайной величины  меньших, чем
меньших, чем 
 объем выборки.
объем выборки.
По определению  обладает следующими свойствами:
обладает следующими свойствами:
1. 
2. Для любых 
3.  при
при 
 при
при 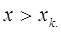
Эмпирическая функция распределения  является оценкой функции распределения
является оценкой функции распределения  которая в этом случае называется теоретической функцией распределения.
которая в этом случае называется теоретической функцией распределения.






