Пусть оценивается некоторый параметр 
наблюдаемой СВ 
генеральной совокупности. Пусть из генеральной совокупности извлечена выборка объема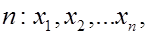 
по которой может быть найдена оценка 
параметра 
.
Например, для нормального закона распределения с плотностью вероятности
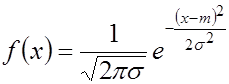параметрами являются математическое ожидание 
и среднее квадратическое отклонение 
.
Точечной оценкой 
параметра 
называется числовое значение этого параметра, полученное по выборке объема 
.
Например, оценками и 
могут быть:
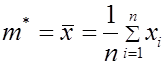и 
соответственно.
Нетрудно заметить, что оценка 
являются функцией от выборки, т.е. 
= 
.
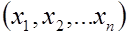Так как выборка носит случайный характер, то оценка 
является СВ, принимающей различные значения для различных выборок. Любую оценку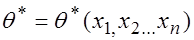 
называют статистикой или статистической оценкой параметра 
Точностью оценки называют такое числ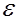о 
, что 
. Естественно стремление получить по возможности наиболее точную оценку при данном объеме выборки.
Приведем свойства, выполнимость которых желательна для того, чтобы оценка была признана удовлетворительной.
В силу случайности точечной оценки 
она может рассматриваться как СВ со своими числовыми характеристиками – математическим ожиданием 
и дисперсией 
Чем ближе 
к истинному значению и чем меньше 
тем лучше будет оценка (при прочих равных условиях). Т.о., качество оценок характеризуется следующими основными свойствами:
- несмещенность;
- эффективность;
Состоятельность.
Оценка 
называется несмещенной оценкой параметра 
, если ее математическое ожидание равно оцениваемому параметру: 
В противном случае – оценка называется смещенной.
Разность 
- называется смещением или систематической ошибкой оценивания. Для несмещенных оценок систематическая ошибка равна нулю. Если 
, то 
завышает среднее значение 
Свойство несмещенности оценки является важнейшим, но не единственным. Существует несколько возможных несмещенных оценок одного и того же параметра. Выбор будет сделан в пользу той из них, вероятность совпадения которой с истинным значением оцениваемого параметра выше. Оценка должна иметь такую плотность вероятности, которая наиболее «сжата» вокруг истинного значения оцениваемого параметра. Нетрудно заметить, что в этом случае она будет иметь наименьшую среди других оценок дисперсию.
Оценка 
называется эффективной оценкой параметра , если ее дисперсия 
меньше дисперсии любой другой альтернативной несмещенной оценки при фиксированном объеме выборки 
т.е. 
Оценка называется асимптотически эффективной, если с увеличением объема выборки ее дисперсия стремится к нулю, т.е. 
при 
∞ (индекс в оценке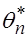 
применяется для подчеркивания объема выборки).
Оценка 
называется состоятельной оценкой параметра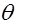 
, если 
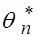сходится по вероятности к оцениваемому параметру 
при ∞. Другими словами, состоятельной называется такая оценка, которая дает истинное значение при достаточно большом объеме выборки вне зависимости от значений входящих в нее конкретных наблюдений.
Справедливо следующее утверждение: если 
и 
при ∞, то 
состоятельная оценка параметра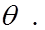 
Оценки, являющиеся линейными функциями от выборочных наблюдений, называется линейными.
Наиболее употребляемыми методами нахождения точечных оценок является метод моментов, метод максимального правдоподобия, метод наименьших квадратов.
