| Номер пары | Значение признаков | Отклонение | Квадраты отклонений | Произведения | |||
| х | у | ( - -  ) )
| ( - -  ) )
| ( - -  )2 )2
| ( - -  )2 )2
| (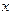 - -  )· ( )· ( - -  ) )
| |
| 1. | |||||||
| 2. | |||||||
| 3. | |||||||
| 4. | |||||||
| 5. | |||||||
| 6. | |||||||
| 7. | |||||||
| 8. | |||||||
| 9. | |||||||
| 10. | |||||||
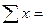
| 
| 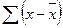
| 
| 
| 
| 
|
1) Вычислите вспомогательные величины:
n =


2) Определите коэффициент корреляции:
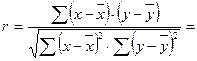
Выводы: _____
______________________________________________________________
3) Определите коэффициент детерминации:
dxy=r2=
Выводы: _____________________________________
4) Вычислите ошибку коэффициента корреляции, критерий значимости и доверительный интервал.

 tr05=
tr05=
r  при v=n-1
при v=n-1
Вывод:
5) Определите коэффициент регрессии bYX и bXY;
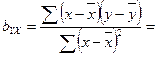

Проверьте правильность вычислений по равенству:
bYX· bXY=r2=
6) Рассчитайте уравнение регрессии:

7) Постройте теоретическую линию регрессии
 Y
Y

X
Рис. Теоретическая линия регрессии
Сделайте общий вывод: ___________________________________________________
________________________________________________________________________________________________________
Приложение 1
Коэффициент перевода массы зерна при различной влажности к массе зерна при влажности 14%
(Культуры: пшеница, ячмень, рожь, овес, гречиха, рис, горох, фасоль, чечевица, чина, нут, кукуруза,
сорго, соя, вика, рыжик)
| Целые проценты влажности | Десятые доли процента влажности | |||||||||
| 1,105 | 1,102 | 1,102 | 1,101 | 1,100 | 1,099 | 1,098 | 1,097 | 1,095 | 1,094 | |
| 1,093 | 1,092 | 1,091 | 1,090 | 1,088 | 1,087 | 1,086 | 1,085 | 1,084 | 1,083 | |
| 1,081 | 1,080 | 1,079 | 1,078 | 1,077 | 1,076 | 1,074 | 1,073 | 1,072 | 1,071 | |
| 1,070 | 1,069 | 1,067 | 1,066 | 1,065 | 1,064 | 1,063 | 1,062 | 1,060 | 1,059 | |
| 1,058 | 1,057 | 1,056 | 1,055 | 1,053 | 1,052 | 1,051 | 1,050 | 1,049 | 1,048 | |
| 1,047 | 1,045 | 1,044 | 1,043 | 1,042 | 1,041 | 1,040 | 1,038 | 1,037 | 1,036 | |
| 1,035 | 1,034 | 1,033 | 1,031 | 1,030 | 1,029 | 1,028 | 1,027 | 1,026 | 1,024 | |
| 1,023 | 1,022 | 1,021 | 1,020 | 1,019 | 1,017 | 1,016 | 1,015 | 1,014 | 1,013 | |
| 1,012 | 1,010 | 1,009 | 1,008 | 1,007 | 1,006 | 1,005 | 1,003 | 1,002 | 1,001 | |
| 1,000 | 0,999 | 0,998 | 0,997 | 0,995 | 0,994 | 0,993 | 0,992 | 0,991 | 0,990 | |
| 0,988 | 0,987 | 0,986 | 0,985 | 0,984 | 0,983 | 0,981 | 0,980 | 0,979 | 0,978 | |
| 0,977 | 0,976 | 0,974 | 0,973 | 0,972 | 0,971 | 0,970 | 0,969 | 0,967 | 0,966 | |
| 0,965 | 0,964 | 0,963 | 0,962 | 0,960 | 0,959 | 0,958 | 0,957 | 0,956 | 0,955 | |
| 0,953 | 0,952 | 0,951 | 0,950 | 0,949 | 0,948 | 0,947 | 0,945 | 0,944 | 0,943 | |
| 0,942 | 0,941 | 0,940 | 0,938 | 0,937 | 0,936 | 0,935 | 0,934 | 0,933 | 0,931 | |
| 0,930 | 0,929 | 0,928 | 0,927 | 0,926 | 0,924 | 0,923 | 0,922 | 0,921 | 0,920 | |
| 0,919 | 0,917 | 0,916 | 0,915 | 0,914 | 0,913 | 0,912 | 0,910 | 0,909 | 0,908 | |
| 0,907 | 0,906 | 0,905 | 0,903 | 0,902 | 0,901 | 0,900 | 0,899 | 0,898 | 0,896 | |
| 0,895 | 0,894 | 0,893 | 0,892 | 0,891 | 0,890 | 0,888 | 0,887 | 0,886 | 0,885 | |
| 0,884 | 0,882 | 0,881 | 0,880 | 0,879 | 0,878 | 0,877 | 0,876 | 0,874 | 0,873 | |
| 0,872 | 0,871 | 0,870 | 0,869 | 0,867 | 0,866 | 0,865 | 0,864 | 0,863 | 0,862 |
Приложение 2
Стандартные значения критерия t (критерий Стьюдента)
| Число степеней свободы | Уровень значимости | Число степеней свободы | Уровень значимости | ||
| 12,7 | 63,7 | 2,2 | 3,0 | ||
| 4,3 | 9,9 | 14-15 | 2,1 | 3,0 | |
| 3,2 | 5,8 | 16-17 | 2,1 | 2,9 | |
| 2,8 | 4,6 | 18-20 | 2,1 | 2,9 | |
| 2,6 | 4,0 | 21-24 | 2,1 | 2,8 | |
| 2,4 | 3,7 | 25-28 | 2,1 | 2,8 | |
| 2,4 | 3,5 | 29-30 | 2,0 | 2,8 | |
| 2,3 | 3,4 | 31-34 | 2,0 | 2,7 | |
| 2,3 | 3,3 | 35-42 | 2,0 | 2,7 | |
| 2,2 | 3,2 | 43-62 | 2,0 | 2,7 | |
| 2,2 | 3,1 | 63-175 | 2,0 | 2,6 | |
| 2,2 | 3,1 | 176 и больше | 2,0 | 2,6 |
Приложение 3
Стандартные значения критерия F для уровня значимости 05
| Число степеней свободы для меньшей дисперсии (ошибки) | Число степеней свободы для большой дисперсии, которая берется числителем | ||||||||||||
| 18,5 | 19,2 | 19,2 | 19,3 | 19,3 | 19,3 | 19,4 | 19,4 | 19,4 | 19,4 | 19,4 | 19,5 | 19,5 | |
| 10,1 | 9,6 | 9,3 | 9,1 | 9,0 | 8,9 | 8,9 | 8,8 | 8,8 | 8,8 | 8,7 | 8,6 | 8,5 | |
| 7,7 | 6,9 | 6,6 | 6,4 | 6,3 | 6,2 | 6,1 | 6,0 | 6,0 | 6,0 | 5,9 | 5,8 | 5,6 | |
| 6,6 | 5,8 | 5,4 | 5,2 | 5,1 | 5,0 | 4,9 | 4,8 | 4,8 | 4,7 | 4,7 | 4,5 | 4,4 | |
| 6,0 | 5,1 | 4,8 | 4,5 | 4,4 | 4,3 | 4,2 | 4,2 | 4,1 | 4,1 | 4,0 | 3,8 | 3,7 | |
| 5,6 | 4,7 | 4,4 | 4,1 | 4,0 | 3,9 | 3,8 | 3,7 | 3,7 | 3,6 | 3,6 | 3,4 | 3,2 | |
| 5,3 | 4,5 | 4,1 | 3,8 | 3,7 | 3,6 | 3,5 | 3,4 | 3,4 | 3,3 | 3,3 | 3,1 | 2,9 | |
| 5,1 | 4,3 | 3,9 | 3,6 | 3,5 | 3,4 | 3,3 | 3,2 | 3,2 | 3,1 | 3,1 | 2,9 | 2,7 | |
| 5,0 | 4,1 | 3,7 | 3,5 | 3,3 | 3,2 | 3,1 | 3,1 | 3,0 | 3,0 | 2,9 | 2,7 | 2,5 | |
| 4,8 | 4,0 | 3,6 | 3,4 | 3,2 | 3,1 | 3,0 | 3,0 | 2,9 | 2,9 | 2,8 | 2,6 | 2,4 | |
| 4,8 | 3,9 | 3,5 | 3,3 | 3,1 | 3,0 | 2,9 | 2,8 | 2,8 | 2,8 | 2,7 | 2,5 | 2,3 | |
| 4,7 | 3,8 | 3,4 | 3,2 | 3,0 | 2,9 | 2,8 | 2,8 | 2,7 | 2,7 | 2,6 | 2,4 | 2,2 | |
| 4,6 | 3,7 | 3,3 | 3,1 | 3,0 | 2,9 | 2,8 | 2,7 | 2,6 | 2,6 | 2,5 | 2,3 | 2,1 | |
| 4,5 | 3,7 | 3,3 | 3,1 | 2,9 | 2,8 | 2,7 | 2,6 | 2,6 | 2,6 | 2,5 | 2,3 | 2,1 | |
| 4,5 | 3,6 | 3,2 | 3,0 | 2,9 | 27, | 2,7 | 2,6 | 2,6 | 2,5 | 2,4 | 2,2 | 2,0 | |
| 4,5 | 3,6 | 3,2 | 3,0 | 2,8 | 2,7 | 2,6 | 2,6 | 2,5 | 2,4 | 2,4 | 2,2 | 2,0 | |
| 4,4 | 3,6 | 3,2 | 2,9 | 2,8 | 2,7 | 2,6 | 2,5 | 2,5 | 2,4 | 2,3 | 2,1 | 1,9 | |
| 4,4 | 3,5 | 3,1 | 2,9 | 2,7 | 2,6 | 2,6 | 2,5 | 2,4 | 2,4 | 2,3 | 2,1 | 1,9 |
Приложение 4
Стандартные значения критерия F для уровня значимости 01
| Число степеней свободы для меньшей дисперсии (ошибки) | Значения критерия при числе степеней свободы для большей дисперсии, которая берется числителем | ||||||||||||
| 98,5 | 99,0 | 99,2 | 99,3 | 99,3 | 99,3 | 99,3 | 99,3 | 99,4 | 99,4 | 99,4 | 99,5 | 99,5 | |
| 34,1 | 30,8 | 29,5 | 28,7 | 28,2 | 27,9 | 27,7 | 27,5 | 27,3 | 27,2 | 27,1 | 26,6 | 26,1 | |
| 21,2 | 18,0 | 16,7 | 16,0 | 15,8 | 15,2 | 15,0 | 14,8 | 14,7 | 14,5 | 14,4 | 13,9 | 13,5 | |
| 16,3 | 13,3 | 12,1 | 11,4 | 11,0 | 10,7 | 10,4 | 10,3 | 10,2 | 10,0 | 9,9 | 9,5 | 9,0 | |
| 13,7 | 10,9 | 9,8 | 9,2 | 8,8 | 8,5 | 8,0 | 8,1 | 8,0 | 7,9 | 7,7 | 7,3 | 6,9 | |
| 12,3 | 9,6 | 8,5 | 7,9 | 7,5 | 7,2 | 7,0 | 6,8 | 6,7 | 6,6 | 6,5 | 6,1 | 5,1 | |
| 11,3 | 8,7 | 7,6 | 7,0 | 6,6 | 6,4 | 6,2 | 6,0 | 5,9 | 5,8 | 5,7 | 5,3 | 4,9 | |
| 10,6 | 8,0 | 7,0 | 6,4 | 6,1 | 5,8 | 5,6 | 5,5 | 5,4 | 5,3 | 5,1 | 4,7 | 4,3 | |
| 10,0 | 7,6 | 6,6 | 6,0 | 5,6 | 5,4 | 5,2 | 5,1 | 5,0 | 4,8 | 4,7 | 4,3 | 3,9 | |
| 9,7 | 7,2 | 6,2 | 5,7 | 5,3 | 5,4 | 4,9 | 4,7 | 4,6 | 4,5 | 4,4 | 4,0 | 3,6 | |
| 9,3 | 6,9 | 6,0 | 5,4 | 5,1 | 4,8 | 4,6 | 4,5 | 4,4 | 4,3 | 4,2 | 3,8 | 3,4 | |
| 9,1 | 6,7 | 5,7 | 5,2 | 4,9 | 4,6 | 4,4 | 4,3 | 4,2 | 4,1 | 4,0 | 3,6 | 3,2 | |
| 8,9 | 6,5 | 5,6 | 5,0 | 4,7 | 4,5 | 4,3 | 4,1 | 4,0 | 3,9 | 3,8 | 3,4 | 3,0 | |
| 8,7 | 6,4 | 5,4 | 4,9 | 4,6 | 4,3 | 4,1 | 4,0 | 3,9 | 3,8 | 3,7 | 3,3 | 2,9 | |
| 8,5 | 6,2 | 5,3 | 4,8 | 4,4 | 4,2 | 4,0 | 3,9 | 3,8 | 3,7 | 3,6 | 3,2 | 2,8 | |
| 8,4 | 6,1 | 5,2 | 4,7 | 4,3 | 4,1 | 3,9 | 3,8 | 3,7 | 3,6 | 3,5 | 3,1 | 2,7 | |
| 8,3 | 6,3 | 5,1 | 4,6 | 4,3 | 4,0 | 3,8 | 3,7 | 3,6 | 3,5 | 3,4 | 3,0 | 2,6 | |
| 8,2 | 5,9 | 5,0 | 4,5 | 4,2 | 3,9 | 3,8 | 3,6 | 3,5 | 3,4 | 3,3 | 2,9 | 2,5 |
ЛИТЕРАТУРА
1. Доспехов Б.А. Методика полевого опыта/ Б.А. Доспехов. – М.: Агропромиздат, 1985. – 351 с.
2. Кащеев А.Н. Основы научных исследований в агрономии (для лаб.-практич. занятий): учебное пособие для вузов/ А.Н. Кащев. Пензен. гос. с. – х. акад. – Пенза: РИО ПГСХА, 2001. – 126с.
3. Методические указания к практическим занятиям и самостоятельной работе студентов по основам научных исследований в растениеводстве. – Омск: ОмСХИ, 1990.-48с.
4. Моисейченко В.Ф., Трифонова М.Ф., Заверюха А.Х. Основы научных исследований в агрономии. – М.: Колос, 1996. – 386с.
ОГЛАВЛЕНИЕ
| Введение……………………………………………………………….. | |
| 1 Планирование и проведение исследования……………………….. | |
| Задание 1.1 Планирование исследования по выбранной теме и учёт урожая в опыте……………………………………………………. | |
| 2 Основы статистического анализа результатов опыта……………... | |
| Задание 2.1 Группировка и статистическая обработка данных количественной изменчивости…………………………………… | |
| Задание 2.2 Статистическая обработка экспериментальных данных дробных методом…………………………………………………. | |
| Задание 2.3 Статистическая обработка данных однофакторного полевого опыта методом дисперсионного анализа…………….. | |
| Задание 2.4 Статистическая обработка данных урожайности двухфакторного полевого опыта методом дисперсионного анализа…………………………………………………………….. | |
| Задание 2.5 Корреляционный и регрессионный анализ……………………………….…………………………………. | |
| Приложение 1 Коэффициент перевода массы зерна при различной влажности к массе зерна при влажности 14%………………………………………………………………… | |
| Приложение 2 Стандартные значения критерия t (критерий Стьюдента)……………………………………………………………… | |
| Приложение 3Стандартные значения критерия F для уровня значимости 05………………………………………………………… | |
| Приложение 4 Стандартные значения критерия F для уровня значимости 01………………………………………………………… | |
| Литература……………………………………………………………... |






