МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение
Высшего профессионального образования
«СЕВЕРО-КАВКАЗСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
ПО ДИСЦИПЛИНЕ
ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ И МОДЕЛИ
В ЗАДАЧАХ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Направление подготовки 010100.68 «Математика»
Профиль подготовки (специализация)
Вычислительная математика
Квалификация (степень) выпускника
Магистр
Редькина Т.В.
Ставрополь, 2012
Пояснительная записка
Настоящие пособие предназначено для студентов математических специальностей как очной, так и заочной форм обучения.
Вычислительные методы и модели в задачах математической физики является мощным математическим инструментом, широко используемым при решении многих прикладных задач. В тоже время недостаточная подготовленность в этой области приводит к неэффективности использования возможностей применения численных методов, а то и к прямым ошибкам. Это связано в первую очередь с качественным отличием изучаемой дисциплины от других математических предметов, что способствует возникновению «психологических трудностей» при использовании соответствующих математических методов и приемов. Все перечисленное обуславливает необходимость предлагаемого пособия. При этом важно иметь в виду, что вычислительная математика должна изучаться студентами нематематических специальностей в соответствии с требованиями Государственного образовательного стандарта.
Предлагаемое пособие является дополнением к материалу, изучаемому на занятиях, а также направлено на обеспечение возможности самостоятельной работы студентов, особенно студентов заочной формы обучения.
Кроме изложения теоретического материала предложены 14 вариантов самостоятельных работ, включающих задания по всем рассматриваемым вопросам. При этом подробные решения аналогичных примеров, приведенные в данном пособии, позволят студентам самостоятельно освоить методы их решения или же закрепить навыки, полученные на лекционных занятиях.
Подобранный дидактический материал может быть использован также как сборник лабораторных работ по вычислительной математике.
Практическое занятие № 1
Приближенные методы работы со скалярными функциями
Определение погрешностей вычислений и обратная задача
Целью является формирование:
- Способности работать самостоятельно, забота о качестве, стремление к успеху (ОК-6)
- Способности порождать новые идеи (ОК-5)
- Умения ориентироваться в современных алгоритмах компьютерной математики, совершенствовать, углублять и развивать математическую теорию, лежащую в их основе (ПК-7)
- Умения делать самостоятельный анализ физических аспектов в классических постановках математических задач (ПК-4)
- Умения определять общие формы закономерностей, инструментальных средств для групп дисциплин (ПК-10)
Теоретические основы
Операторы и операнды
Операторы — элементы языка, предназначенные для создания математических выражений совместно с данными, именуемыми операндами. Это знаки арифметических операций, вычисления сумм и произведений членов ряда, производных, интегралов и т. д. После указания операндов (аргументов соответствующих операторов) операторы становятся исполняемыми программными блоками. Mathcad позволяет задавать и пользовательские операторы. Операторы в Mathcad вводятся с помощью шаблонов, которые, в свою очередь, имеют места ввода для операндов.
Математические выражения
Функции наряду с операторами могут входить в математические выражения. Например, рассмотрим выражение: Y: = 5 - lп (х) + 1
В этом выражении Y — переменная, 1 и 5 — числовые константы, • и + — операторы, lп (х) — встроенная функция.
При выполнении символьных операций константы p и е используются только в символьном виде. Это значит, что их численные значения не вычисляются при выводе результатов символьных вычислений. К примеру, число 2 p = 6. 283... при использовании знака символьного вычисления ® выводится как 2 p, а не как приближенное численное значение, при использовании же знака = будет получено 6.283.
Переменные
Назначение переменных в Mathcad соответствует назначению переменных в математике. Уже само их название говорит о том, что значения переменных могут меняться. Они используются для обобщенного представления данных определенного типа. К примеру, вычисление значения выражения (2 + 3), равного 5, носит весьма частный характер. Куда более общим является вычисление значения выражения (х + у) как суммы значений двух переменных — х и у. В частности, при х = 1 и у = 3 для (х + у) получим значение 4, но уже при х = 3 и у = 5 вычисление (х + у) даст 8.
Переменные имеют имена — идентификаторы. В нашем случае это х и у. Однако Mathcad позволяет задавать и более сложные имена, например Х_coordinate, Vcub и т. д. Длина идентификатора не ограничена. Внутри мен переменных надо избегать знаков, которые могут трактоваться как операторы (например, пробел, *, /, +, - и т. д.). Имена должны начинаться с буквы (допустимо а 2, но не 2 а и т. д.).
Функции
Mathcad поддерживает множество встроенных функций, то есть функций, определенных в самой системе и готовых к немедленному использованию. Функции обладают свойством возвращать некоторое значение в ответ на обращение к ним по имени с указанием аргумента (или списка аргументов). Они возвращают символьное или числовое значение, вектор или матрицу. В систему встроен ряд элементарных математических функций, например функция вычисления синуса sin(х), натурального логарифма lп (х) и т. д.
Функции вводятся своими именами, принятыми в системе Mathcad. Иногда эти имена несколько отличаются от стандартных обозначений — в основном некоторым сокращением. К примеру, arctg(x) в Mathcad обозначается как atan(x). При вводе функции посредством палитры функций появляется шаблон для ввода параметров. Если на имени функции установлен курсор ввода, то нажатие клавиши F1 открывает страницу справки по указанной функции.
Возможно также задание функций пользователя, которые создаются самим пользователем. Благодаря функциям пользователя обеспечивается расширение входного языка Mathcad и его адаптация к специфическим задачам пользователя.
Набор функций системы Mathcad может дополняться с помощью корректирующих систему Patch-файлов, загружаемых библиотек функций, пакетов расширений и электронных книг.
Погрешность вычислений
Погрешность — разность х — а, где а — данное число, которое рассматривается как приближенное значение некоторой величины, точное значение которой равно х. Разность х — а называется также абсолютной погрешностью. Отношение х — а к а называется относительной погрешностью числа а. Для характеристики погрешности обычно пользуются указанием ее границ. Число D(а) такое, что | х — а | ≤ D(а), называется границей абсолютной погрешности. Число d (а)такое, что  , наз. границей относительной погрешности. Границы относительной погрешности часто выражают в процентах. В качестве D(а) и d (а)берутся по возможности меньшие числа.
, наз. границей относительной погрешности. Границы относительной погрешности часто выражают в процентах. В качестве D(а) и d (а)берутся по возможности меньшие числа.
Информацию о том, что число а является приближенным значением числа х с границей абсолютной погрешности D(а), принято записывать в виде х = а ± D(а). Аналогичное соотношение для относительной погрешности записывается в виде х = а (l ± d (а)).
Границы абсолютной и относительной погрешности указывают на максимально возможное расхождение х и а. Наряду с ними часто употребляются характеристики погрешности, учитывающие характер возникновения (напр., погрешность измерений) и частоту различных значений разности х и а. При таком подходе используются методы теории вероятностей. При численном решении задачи результата обуславливается неточностями, которые присущи формулировке задачи и способам ее решения. Погрешность, возникающую вследствие неточности математического описания реального процесса, называют погрешностью математической модели; возникающую вследствие неточности задания исходных данных — называют погрешностью входных данных; возникающую вследствие неточности метода решения — погрешностью метода; возникающую вследствие неточности вычислений — вычислительной погрешностью. В процессе вычислений исходные погрешности последовательно переходят от операции к операции, накапливаясь и порождая новые. Возникновение и распространение погрешностей в вычислениях являются предметом специальных исследований курса Вычислительной математики.
Обратная задача теории погрешностей
Обратная задача заключается в том, чтобы определить с какой точностью надо взять каждый параметр расчетной формулы, чтобы погрешность результата не превышала заданной величины  . Очевидно, эта задача однозначно не разрешима, поэтому возможны несколько вариантов однозначной разрешимости поставленной проблемы.
. Очевидно, эта задача однозначно не разрешима, поэтому возможны несколько вариантов однозначной разрешимости поставленной проблемы.
Будем рассматривать расчетную формулу вида  , тогда абсолютная погрешность искомой функции определяется по формуле
, тогда абсолютная погрешность искомой функции определяется по формуле
 , (1)
, (1)
а формула расчета относительной погрешности имеет вид
 . (2)
. (2)
Зная  найдем все
найдем все 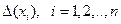 .
.
I. Предположим, что  - постоянная величина для всех
- постоянная величина для всех 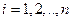 , тогда формула (1) примет вид:
, тогда формула (1) примет вид:  . Из полученного равенства определяется абсолютная погрешность
. Из полученного равенства определяется абсолютная погрешность 
 .
.
II. Найдем  , предполагая что
, предполагая что  - постоянная величина. Равенство (1) с учетом выдвинутых предположений примет вид:
- постоянная величина. Равенство (1) с учетом выдвинутых предположений примет вид: 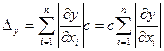 , следовательно
, следовательно

III. Предположим, что 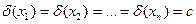 - постоянная величина. По определению относительной погрешности имеем
- постоянная величина. По определению относительной погрешности имеем
 , (3)
, (3)
следовательно  . Используя формулу (1) получаем
. Используя формулу (1) получаем
 .
.
Определим из последнего равенства постоянную с
 ,
,
в силе соотношения (3) определяем  , или окончательно
, или окончательно
 .
.
Теоретические вопросы, выносимые на обсуждение
1. Что является предметом исследований курса вычислительной математики.
2. Дайте определение оператора в математике и программировании.
3. Что такое операнды.
4. Как производится ввод операторов в программе Mathcad.
5. Где можно найти операторы в программе Mathcad.
6. Как производится ввод математических выражений.
7. Как различаются переменные и функции.
8. Как можно использовать постоянные специального вида: p и е.
9. Какая запись используется, чтобы найти численные значения выражении, содержащих постоянные специального вида: p и е.
10. Какая запись используется, чтобы получить символьную запись значения выражения, содержащего постоянные специального вида: p и е.
11. Каково назначение переменных в Mathcad.
12. Что такое идентификаторы.
13. Какой вид могут иметь идентификаторы.
14. Чем ограничивается длина идентификатора.
15. Какие элементы следует избегать при записи идентификаторов.
16. Каково самое главное отличие идентификатора от математического выражения.
17. Какие функции называются встроенные.
18. Приведите пример и продемонстрируйте некоторые встроенные функции.
19. Как вводятся встроенные функции.
20. Как используется палитра функций для ввода параметров математического выражения.
21. Как вызвать справку по указанной функции.
22. Как можно пополнять набор функций системы Mathcad.
23. Дать определение абсолютной погрешности.
24. Дать определение относительной погрешности.
25. Что называется границей абсолютной погрешности.
26. Что называется границей относительной погрешности.
27. Как записывается число с заданной абсолютной погрешностью D а.
28. Как записывается число с заданной относительной погрешностью dа.
29. На что указывают границы абсолютной и относительной погрешности.
30. Перечислите, какие виды характеристик погрешности, связанные с источником их возникновения, вы знаете.
31. Запишите формулу для расчета абсолютной погрешности функции вида  .
.
32. Запишите формулу для расчета относительной погрешности функции вида  .
.
33. Дайте определение обратной задачи теории погрешностей.
34. Однозначно ли разрешима обратная задача теории погрешностей.
35. Перечислите, какие варианты однозначной разрешимости обратной задачи вы знаете.
36. Выведите расчетную формулу для решения обратной задачи в случае  - постоянная величина для всех
- постоянная величина для всех 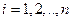 .
.
37. Выведите расчетную формулу для решения обратной задачи в случае  - постоянная величина.
- постоянная величина.
38. Выведите расчетную формулу для решения обратной задачи в случае 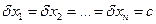 - постоянная величина.
- постоянная величина.
Задания к вариантам для самостоятельных работ
I. Принадлежат ли указанные значения переменных с заданными погрешностями области допустимых значений функции. Вычислить значение функции и ее относительную и абсолютную погрешность:
1.  ,
,
при 

2.  ,
,
при 

3. 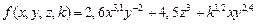 ,
,
при 

4.  ,
,
при 
 .
.
5. 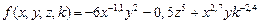 ,
,
при 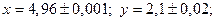

6.  ,
,
при 

7. 
при 

8.  ,
,
при 

9.  ,
,
при 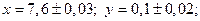

10.  ,
,
при 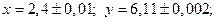

11.  ,
,
при 

12. 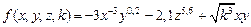 ,
,
при 

13.  ,
,
при 

14.  ,
,
при 
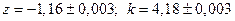
II Определить скорость роста функции в направлении каждой переменной. Округлить заданные значения переменных до десятых долей, вычислить значение функции и найти погрешность, с которой оно вычислено
1.  , при
, при 
2.  , при
, при 
3.  , при
, при 
4. 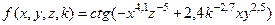 , при
, при 
5.  , при
, при 
6.  , при
, при 
7.  , при
, при 
8.  , при
, при 
9.  , при
, при 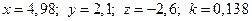
10.  , при
, при 
11.  , при
, при 
12.  , при
, при 
13.  , при
, при 
14.  , при
, при 
III С какой точностью надо взять каждый параметр расчетной формулы, чтобы погрешность не превосходила заданного числа  в случае а).
в случае а).  ; б).
; б).  , в).
, в).  .
.
Охарактеризовать, какой случай более выгоден для заданной функции, обосновать вывод и подтвердить расчетами.
1.  ,
,  , при
, при 
2.  ,
,  , при
, при 
3.  ,
,  при
при 
4. 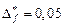 ,
,  , при
, при 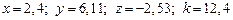
5.  ,
,  , при
, при 
6.  ,
,  , при
, при 
7.  ,
,  , при
, при 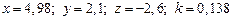
8.  ,
, 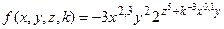 , при
, при 
9.  ,
,  , при
, при 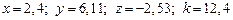
10. 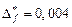 ,
,  , при
, при 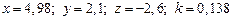
11.  ,
,  , при
, при 
12.  ,
,  , при
, при 
13.  ,
,  , при
, при 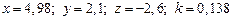
14.  ,
,  , при
, при 
Практическое занятие № 2






