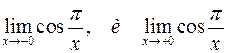1. Найти предел, используя деление на х в максимальной степени.
2. Найти предел, используя сокращение на 
.
3. Найти предел, используя перевод иррациональности, например, из числителя в знаменатель.
4. Найти предел, используя преимущественно первый замечательный предел.
5. Найти предел, используя преимущественно второй замечательный предел.
6. Найти предел, используя преимущественно понятие эквивалентности бесконечно малых (символ «о» - малое).
Ответы
1.
2.
3.
4.
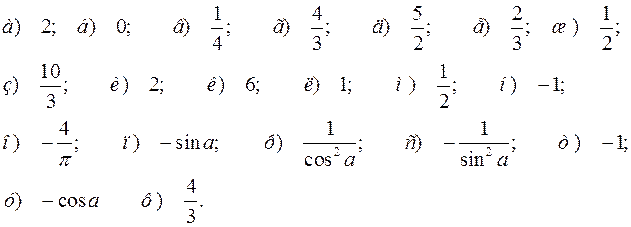
5.
6.
ГЛАВА 4
Непрерывность функций
1. Понятие непрерывности. Пусть функция определена в некоторой окрестности точки 
. Функция 
называется непрерывной в точке 
, если
(1)
или, что равносильно следующей формулировке: функция называется непрерывной в точке , если предел приращения функции при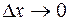 
равен нулю. Математическая запись этого утверждения:
.
Если функция определена в правой (левой) полуокрестности точки 
, то непрерывность понимается как непрерывность справа (слева):
,
(
- для непрерывности слева).
Для того чтобы функция была непрерывна в точке 
, необходимо и достаточно, чтобы она была непрерывна в этой точке справа и слева.
2. Основные свойства непрерывных функций:
2.1. Если 
, 
непрерывны в точке , то 
, 
, 
при 
(для частного функций) также непрерывны в точке .
2.2. Пусть функция 
определена на множестве 
, а 
- множество значений этой функции, и пусть 
определена на 
. Тогда, если функция 
непрерывна в точке 
, а функция непрерывна в точке 
, где 
, то сложная функция 
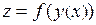непрерывна в точке .
2.3. Обратная функция 
для монотонной непрерывной функции также непрерывна и монотонна на множестве 
.
2.4. Все основные элементарные функции 
, 
, 
(
), 
, 
, 
, 
, 
, 
, 
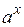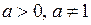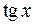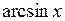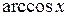- являются непрерывными в своей области определения.
Элементарные функции, то есть функции, получаемые из основных элементарных функций с помощью арифметических операций и вычисления сложных функций, также непрерывны в области определения.
3. Основные теоремы о непрерывных функциях.
1 -я теорема Больцано-Коши. Если функция непрерывна на отрезке 
и на концах его имеет значения, противоположные по знаку, то обращается в нуль по крайней мере в одной точке интервала 
.
2 -я теорема Больцано-Коши. Пусть функция непрерывна на отрезке , причем 
. Тогда каким бы ни было число С, заключенное между числами А и В, на отрезке найдется по крайней мере одна точка с, такая, что 
.
1-я теорема Вейерштрасса. Если функция 
непрерывна на отрезке , то она ограничена на нем сверху и снизу, т.е. существуют такие числа 
, что для всех 
верно неравество 
2 -я теорема Вейерштрасса. Если функция непрерывна на отрезке , то она достигает на этом отрезке своих точной нижней и верхней граней, т.е. на отрезке найдутся такие точки 
4. Точки разрыва функции. Их классификация.
Предельной точкой x 0 для множества Х называется такая точка, в любой окрестности которой имеются точки из Х, отличные от х 0. Заметим, что сама предельная точка может и не принадлежать множеству X.
Пусть x 0 - предельная точка области определения функции.
Точка называется точкой разрыва функции, если функция не определена в этой точке или не является непрерывной, то есть формула (1) не имеет места.
1) называется точкой устранимого разрыва, если существует 
, но либо не определена в точке , либо 
.
В этом случае всегда можно доопределить функцию до непрерывной, то есть в точке положить 
равной .
2) - точка разрыва первого рода (разрыв скачком) если существуют левый-правый пределы 
, но 
.
Величина 
называется скачком функции.
3) остальные точки разрыва называются точками разрыва второго рода, то есть точки , в которых не существует хотя бы один из односторонних пределов.
Примеры решения задач
ПРИМЕР 1. Исследовать функцию 
на непрерывность в точке 
Решение. Для данной функции точка 
есть точка разрыва второго рода. Это обнаруживается при нахождении правостороннего предела.
Левосторонний предел оказывается конечной величиной
ПРИМЕР 2. Доказать, что функция 
непрерывна для любого значения аргумента 
Решение. Имеем
Так как 
то при любом 
имеем: 
ПРИМЕР 3. Является ли функция 
разрывной?
Решение. Функция разрывна при 
Эта функция не определена в точке 
и, как бы мы ни выбирали число 
, пополненная функция 
не будет непрерывной при
ПРИМЕР 4. Определить точки разрыва и исследовать характер точек, если 
.
Решение. Функция имеет разрыв 1-рода при . В самом деле, здесь 
ПРИМЕР 5. Определить точки разрыва и исследовать характер точек, если 
Решение. Функция 
в точке имеет разрыв 2-го рода, так как здесь не существуют оба односторонних предела: 
