Полученные ранее формулы (3.19), (3.20) и (3.21) являются определяющими для нахождения аналитических выражений для частотных характеристик.
Апериодическое звено
W(jw) = 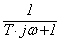 =
=  =
=  - j
- j 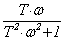 , (3.55)
, (3.55)
т.е. U(w) =  ; V(w) =
; V(w) = 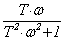 .
.
A(w) = 
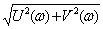 =
=  ; (3.56)
; (3.56)
j(w) = arctg  = - arctg wT. (3.57)
= - arctg wT. (3.57)
АЧХ и ФЧХ звенья показаны на рис. 3.12.
|
Из рис. 3.12 следует, что апериодическое звено обладает свойством фильтра высоких частот и при изменении частоты от 0 до ¥ сдвиг по фазе изменяется от 0 до -90°.
Если АЧХ и ФЧХ этого звена сняты экспериментально, то на частоте w = 1/Т, A(1/T)=  , j(1/T)=-45°. Поэтому значения эти легко найти. Следовательно, по полученным характеристикам можно найти параметры звена (К и Т).
, j(1/T)=-45°. Поэтому значения эти легко найти. Следовательно, по полученным характеристикам можно найти параметры звена (К и Т).
АФХ может быть построена по формуле (3.55) при изменении частоты от 0 до ¥. Это обусловлено тем, что для частотных характеристик линейных звеньев и систем
U(-w)=U(w), V(-w)=-V(w).
|
Это значит, что АФХ симметрична относительно действительной оси в диапазонах частот от 0 до + ¥ и от - ¥ до 0.
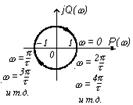
АФХ апериодического звена показана на рис.3.13.
Отметим, что для линейных систем и звеньев строятся асимптотические ЛАЧХ. Рассмотрим методику этого построения для апериодического звена.
Используя выражение (3.56), найдем соотношение для ЛАЧХ в децибелах (дБ).
L(w)=20lg  =20lg1-20lg
=20lg1-20lg 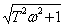 . (3.58)
. (3.58)
Найдем асимптотическое представление для (3.58). Для этого рассмотрим два диапазона частот.
Для 0 £ w < 1/T L(w)» 20lg1. (3.59)
Для 1/T £ w < ¥ L(w)» 20lg1 - 20lgwT=-20lgwT. (3.60)
Выражения (3.59) и (3.60) представляет собой уравнения прямых линий (асимптот точной ЛАЧХ). Низкочастотная асимптота (3.59) горизонтальна и совпадает с осью частот, а высокочастотная асимптота (3.60) является наклонной прямой линией. Эти асимптоты сопрягаются (соединяются) на частоте сопряжения.
Выясним, с каким наклоном на плоскости ЛАЧХ проводится асимптота (3.60). Для этого найдем изменение ординаты этой асимптоты при десятикратном изменении частоты, т.е. найдем наклон прямой в размерности дБ/дек:
L(10w) - L(w) = 20lg1 - 20lg(10wT) - 20lg1 - 20lgwT = -20lg 10 = -20 дБ,
а это означает, что наклон этой асимптоты равен -20 дБ/дек.
Максимальная погрешность аппроксимации имеет место при wсопр=1/Т и равна 20lg 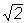 » 3 дБ.
» 3 дБ.
ЛЧХ апериодического звена построены на рис. 3.14.
|
Для интегрирующего звена
W(jw) = 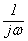 =
=  ,
,
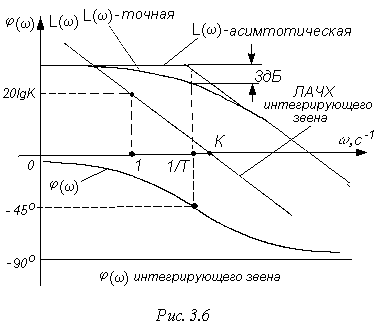
т.е. A(w)= 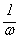 и j(w)=-p/2, что отображено на рис. 3.14.
и j(w)=-p/2, что отображено на рис. 3.14.
Обратим внимание на то, что интегрирующее звено дает постоянный сдвиг по фазе, равный -90° при всех значениях частот.
ЛАЧХ определяется выражением
-20lg A(w) = 20lg 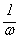 = 20lg1 - 20lg w. (3.61)
= 20lg1 - 20lg w. (3.61)
Выражение (3.61) - уравнение прямой линии, имеющей наклон -20 дБ/дек на плоскости ЛАЧХ при всех значениях частот. Эта линия проходит при w=1с-1 через ординату L(w)=0 дБ (см. рис. 3.14)
ЛЧХ других типовых динамических звеньев приведены в таблице 3.1.
Таблица 3.1.
Характеристика основных элементарных звеньев
| Тип звена | ||||||
| Характе ристика | Пропорциональное (усилительное, безынерционное) | Интегрирующее | Апериодическое (инерционное) | Колебательное | Идеальное дифференцирующее звено | Запаздывающее |
| Уравнение | xвых = k× xвх, где k - коэффициент усиления или передачи звена | 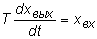 , где Т - постоянная времени , где Т - постоянная времени
|  где k -коэффициент передачи звена, Т - постоянная времени где k -коэффициент передачи звена, Т - постоянная времени
| 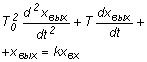 где Т0,Т -постоянные времени, k – ко-эффициент передачи где Т0,Т -постоянные времени, k – ко-эффициент передачи
| 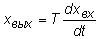 , где Т - постоянная времени , где Т - постоянная времени
| xвых(t - t)= xвх,(t), где t - время запаз-дывания |
| Передаточная функция W(p) | k | 
| 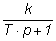
| 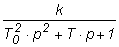
| T× p | 
|
| Переходная характерис-тика h(t) | 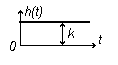
| 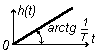
| 
| 
| 
| 
|
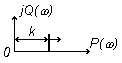
| 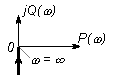
| 
| 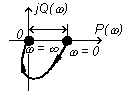
| 
| 
| |
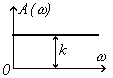
| 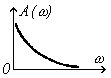
| 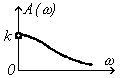
| 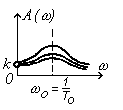
| 
| 
|
Продолжение табл. 3.1.
| Тип звена | ||||||
| Характе-ристика | Пропорциональное (усилительное, безынерционное) | Интегрирующее | Апериодическое (инерционное) | Колебательное | Идеальное диф-ференцирующее звено | Запаздывающее |
| ЛАЧХ L(w) | 
| 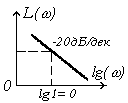
| 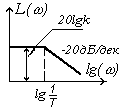
| 
| 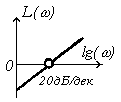
| 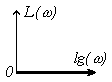
|
| ФЧХ j(w) | 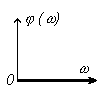
| 
| 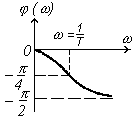
| 
| 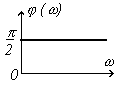
| 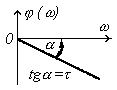
|








