Последовательное соединение. Последовательным соединением звеньев называется такое их соединение, при котором выходная величина предыдущего звена является входной величиной последующего (рис. 2.1).
Необходимо найти W(p)=X(p)/F(p).
|
Из структурной схемы, показанной на рис. 2.1, следуют очевидные соотношения:
|
U(p) = W1(p)·F(p), (2.16)
X(p) = W2(p)·U(p). (2.17)
Подставляя выражение (2.16) для U(p) в формулу (2.17), получим
X(p) = W1(p)· W2(p)· F(p), (2.18)
откуда следует, что
W(p) = X(p)/ F(p) = W1(p)· W2(p). (2.19)
Если последовательно соединены n звеньев, то по аналогии с (2.19) можно записать
, (2.20)
где Õ - знак произведения.
Таким образом, передаточная функция последовательного соединения звеньев равна произведению передаточных функций звеньев, входящих в это соединение.
Параллельное соединение. Параллельным соединением звеньев называется такое их соединение, при котором на входы всех таким образом соединенных звеньев подается одно и то же воздействие, а выходные сигналы суммируются (рис.2.2). Необходимо найти W(p)=X(p)/F(p).
|
Из структурной схемы, показанной на рис. 2.2, следуют очевидные соотношения:
X1(p)=W1(p)·F(p),
X2(p)=W2(p)·F(p).
X(p)=X1(p)+X2(p)=[W1(p)+ W2(p)]·F(p),
W(p)=X(p)/F(p)=W1(p)+ W2(p). (2.21)
Если параллельно соединены n звеньев, то по аналогии с (2.21) можно записать
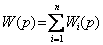. (2.22)
Таким образом, передаточная функция параллельного соединения равна сумме передаточных функций звеньев, входящих в это соединение.
Следует заметить, что при рассматриваемом соединении звеньев, выходные сигналы некоторых из них могут вычитаться. В этом случае выполняется алгебраическое суммирование передаточных функций звеньев.
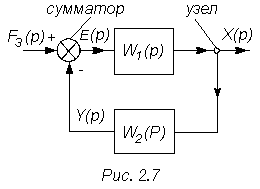
Встречно-параллельное соединение звеньев (замкнутый контур). Встречно-параллельное соединением называется такое соединение звеньев, в котором имеется обратная связь.
|
Рассмотрим простейшую структурную схему, представленную в общем виде на рис. 2.3.
Необходимо найти три передаточные функции замкнутой системы:
1) от fз до x;
2) от fз до y;
3) от fз до e (передаточную функцию ошибки замкнутого контура).
Для того, чтобы понять каким образом необходимо действовать для решения поставленной задачи, подробно рассмотрим получение
.
По структурной схеме, показанной на рис. 2.3, можно записать следующую систему уравнений в изображениях по Лапласу:
E(p) = Fз(p) - Y(p), (2.23)
X(p) = W1(p)E(p), (2.24)
Y(p) = W2(p)X(p). (2.25)
Исключая из уравнений (2.23) - (2.25) переменные E(p) и Y(p), получим операторное уравнение замкнутого контура следующего вида:
[1+W1(p)W2(p)]X(p) = W1(p)Fз(p), (2.26)
откуда получаем искомую передаточную функцию замкнутого контура
. (2.27)
Целесообразно проанализировать передаточную функцию (2.27), используя при этом структурную схему (рис. 2.3).
Назовем передаточную функцию от точки приложения воздействия до точки съема сигнала, считающегося выходным, передаточной функцией прямой цепи передачи воздействия и обозначим ее W П (p). Вся остальная часть контура расположена в цепи обратной связи, и ее передаточная функция W ОС (p).
Для рассмотренного случая (см. рис. 2.3)
WП(p)= W1(p), а WОС(p)= W2(p).
Следовательно, на основе формулы (2.27) передаточную функцию замкнутой системы можно записать так
. (2.28)
Поэтому в каждом конкретном случае для нахождения передаточной функции замкнутого контура необходимо грамотно выделить прямую цепь передачи воздействия и цепь обратной связи, найти их передаточные функции и воспользоваться формулой (2.28).
Воспользуемся этим правилом для определения двух еще не найденных передаточных функций замкнутого контура рис. 2.3. Для этого необходимо мысленно представить исходную структурную схему (рис. 2.3) в виде, показанном на рис. 2.4.
На основе структурной схемы в виде, показанном на рис. 2.4, а, фиксируем, что WП(p) = W1(p)W2(p) и WОС(p) = 1. Поэтому
. (2.29)
Используя структурную схему в виде, показанном на рис. 2.4, фиксируем WП(p)=1 и WОС(p)=W1(p)W2(p). Поэтому
. (2.30)
|
Очень важно научиться находить для каждого из воздействий и сигналов передаточные функции WП(p) и WОС(p), не перечерчивая составленную структурную схему.
Сравним найденные выше передаточные функции Wз1(p), Wз2(p), Wз3(p), определяемые формулами (2.27), (2.28), (2.29). Эти передаточные функции отличаются только числителями, имея один и тот же знаменатель. Это объясняется тем, что один и тот же замкнутый контур не может иметь разные собственные операторы.
Различие числителей полученных передаточных функций показывает, что входная величина по-разному преобразуется в выходную координату в зависимости от места приложения воздействия.
