А) Усилительное безынерционное звено.
На основе формул (3.6), (3.7) и (3.30) переходная и импульсная переходная функции: h(t) = 
= k = const; (3.42)
w(t) = 0. (3.43)
Б) Интегрирующее звено.
На основе формул (3.6), (3.7) и (3.31)
h(t) = 
; (3.42)
w(t) = 
= Ти (3.43)
Графики этих функций показаны на рис. 3.8
|
В) Апериодическое звено.
На основе формул (3.6), (3.7) и (3.32)
h(t) = 
= 1- 
; (3.44)
w(t) = 
= 
. (3.45)
Графики этих функций показаны на рис. 3.9
|
Переходная функция апериодического звена является экспонентой, а поэтому любая подкасательная равна постоянной времени, h(T) = 0,63, h[(3¼5)T]» 1.
Г) Апериодическое звено второго порядка.
В соответствии с (3.6), (3.7) и (3.35) переходная и импульсная переходная функции инерционного звена второго порядка
h(t) = 
=1- 
- 
; (3.46)
w(t) = 
(
- 
). (3.47)
Графики этих функций показаны на рис 3.10.
|
График переходной функции имеет точку перегиба hn(tn), что подтверждает наличие двух устройств (элементов), способных накапливать энергию.
Вычислив вторую производную h(t), найдем координаты точки перегиба переходной функции
= 
= (- 
+ 
),
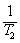
откуда следует, что в точке перегиба
= 
,
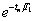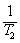
а поэтому
hn = h(tn) = 1- 
.
Угол наклона касательной к переходной функции, проведенной в точке (tn,hn)
tgan = 
= wn(t) =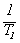 
= 
,
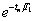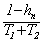т.е. касательная в точке перегиба отсекает на асимптоте h(t)=1 отрезок, равный сумме постоянных времени T1 и T2 (см. рис 3.10,а).
Д.) Колебательное звено
В соответствии с (3.6), (3.7) и (3.35) переходная и импульсная переходная функции колебательного звена (0<x<1)
h(t)= 
= 
; (3.48)
w(t) =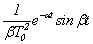 
. (3.49)
Графики этих функций показаны на рис. 3.11.
|
Обратим внимание, что период (затухающих) колебаний
,
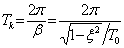где b - частота этих колебаний. Интенсивность затухания колебаний определяется абсолютным значением отрицательной действительной части корней характеристического уравнения. Затухание колебаний за период, как видно из рис.3.11 и выражения (3.48),
,
где m= 
- степень затухания колебаний, что соответствует физической сущности динамических процессов в колебательном звене.
Е) Консервативное звено
В соответствии с (3.48) переходная и импульсная функции консервативного звена
h(t) = 
= (1- cos w 0t) (3.50)
w(t) = w 0× sin w 0t (3.51)
где w 0=1/T0 - частота собственных колебаний, совпадающая с частотой вынужденных колебаний, т.е. имеет место резонанс.
Ж) Дифференцирующее звено
В соответствии с (3.39) и (3.40) переходные функции дифференцирующих звеньев определяются следующими формулами:
для идеального дифференцирующего звена
h(t) = Тд×d(t) = 
; (3.52)
для реального дифференцирующего звена (совпадает с импульсной переходной функцией апериодического звена)
h(t) = 
= 
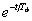, (3.53)
т.е. при t = 0 h(0) = 1.
Импульсная переходная функция реального дифференцирующего звена
w(t) = d(t) - 
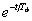× . (3.54)
