Из раздела 2.2, следует, что графическое отображение уравнений САУ представляет собой определенные схемы,. которые называются структурными схемами.
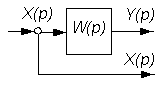
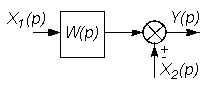
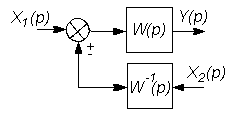
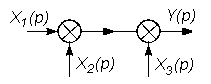
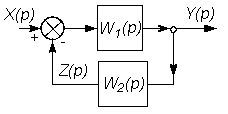
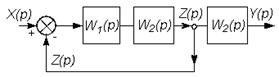
На этих схемах звенья изображаются прямоугольниками, внутри которых записываются передаточные функции. Звенья соединяются линиями, на которых стрелками указывается направление передачи сигнала. На структурных схемах в точках суммирования сигналов изображаются сумматоры, а в точках разветвления сигнала без изменения их величины - узлы (см. рис. 2.3 и 2.4).
Преобразование структурной схемы производится только с целью приведения ее к виду, позволяющему найти необходимые передаточные функции замкнутого контура.
Преобразование структурных схем основано на следующем принципе:
входная и выходная величины преобразуемого участка структурной схемы должны остаться неизменными, так как при соблюдении этого условия исходная и преобразованная структурные схемы являютсяэквивалентными.
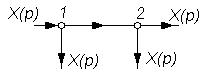
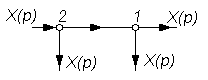
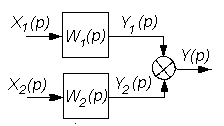
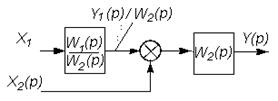
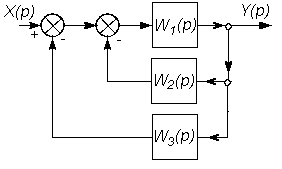
В таблице 2.1 приведены основные правила структурных преобразований.
Таблица 2.1.
Некоторые структурные преобразования
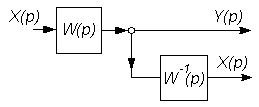
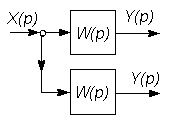
| № п/п | Исходная часть структурной схемы | Преобразованная часть структурной схемы |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
|
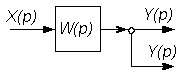
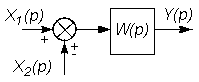
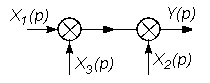
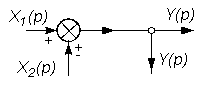
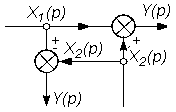
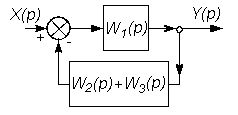
ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЗВЕНЬЕВ И СИСТЕМ
Для анализа линейных звеньев и систем используются временные и частотные характеристики.
Временные характеристики
Временной характеристикой линейного звена или системы называется вынужденная реакция при нулевых начальных условиях, обусловленная типовым воздействием.
Следовательно, временные характеристики при прочих равных условиях зависят от вида типового воздействия. В ТАУ наиболее часто используется два вида типовых воздействий, подаваемых на вход звена или системы.
Единичная ступенчатая функция
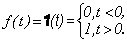(3.1)
График этой функции показан на рис.
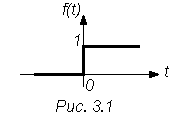
Ступенчатая функция
Изображение по Лапласу ступенчатой функции
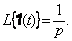(3.2)
Дельта-функция (единичный импульс)
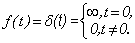(3.3)
Формула (3.3), определяющая эту функцию, показывает, что идеальное импульсное воздействие, представляет собой бесконечно узкий импульс, при этом
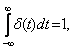(3.4)
поэтому в ТАУ используется термин “единичный импульс”.
Сопоставляя соотношения (3.1) и (3.2), можно сделать вывод, что
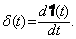(3.5)
Поэтому на основании формулы (3.2) можно записать
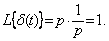
Вынужденная реакция линейного звена или системы на воздействие вида единичной ступенчатой функции называется переходной функцией и обозначается h(t).
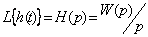, (3.6)
где W(p) - передаточная функция линейного звена или системы.
Вынужденная реакция линейного звена или системы на воздействие видадельта-функции называется импульсной переходной функцией (весовой функцией) и обозначается w(t).
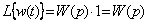. (3.7)
Изображение по Лапласу импульсной переходной функции равно передаточной функции, и в этом важность этой временной характеристики. Действительно, изображение по Лапласу линейной системы на воздействие f(t)
X(p)=W(p)× F(p), (3.8)
во временной области в силу свойств этого преобразования определяется интегралом свертки
, (3.9)
т.е. вынужденная реакция линейного звена или системы в любой текущий момент времени t на воздействие в момент времени t учитывается с весовым коэффициентом w(t - t). Поэтому w(t) часто называют весовой функцией. Иногда эту функцию обозначают через k(t).
Частотные характеристики
Пусть на вход устойчивой системы или звена подается гармонический сигнал вида
f(t) = af× sinwt. (3.10)
Учитывая, что
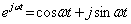, (3.11)
целесообразно найти вынужденную реакцию системы на воздействие вида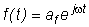 
, (3.12)
а затем учесть мнимую часть этой вынужденной реакции (см. формулы (3.10) и (3.11)).
Линейная система описывается передаточной функцией
,
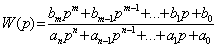т.е. описывается дифференциальным уравнением
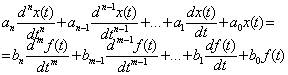
При входном сигнале (3.12) сигнал на выходе найдем в виде
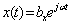. (3.13)
(3.14)
Отношение комплексных амплитуд выходного сигнала (после затухания свободного движения) и входного гармонического сигнала
, (3.15)
называют частотной передаточной функцией (ЧПФ), или комплексным коэффициентом передачи (ККП).
На основании формулы (3.15) можно записать
bx = afW(jw). (3.16)
Используя соотношения (3.10) и (3.11), можно записать
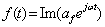. (3.17)
Тогда
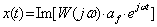. (3.18)
Выделяя в выражении (3.15) действительную и мнимую части, можно записать
W(jw) = Re W(jw) + jIm W(jw) = U(w) + jV(w) = A(w)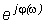 
, (3.19)
где
A(w) =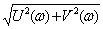 
- модуль ЧПФ, (3.20)
j(w) = arctg(V(w)/U(w)) - аргумент ЧПФ. (3.21)
Выражение (3.18) с учетом (3.19) можно записать в следующем виде
x(t)=Im[A(w)af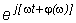 
]= A(w)af × sin[wt+j(w)]=ax × sin[wt+j(w)]. (3.22)
Следовательно, при подаче на вход устойчивой линейной системы гармонического сигнала на ее выходе после затухания свободного движения установится гармонический сигнал с той же частотой, но амплитудой
ax = A(w)af (3.23)
и со сдвигом по фазе
j(w) = arg W(jw).
Соотношения (3.22) и (3.23) позволяют установить физический смысл модуля и аргумента ЧПФ.
Модуль ЧПФ есть отношение амплитуд выходного и входного сигналов системы в режиме установившихся гармонических колебаний на данной частоте.
Аргумент ЧПФ - сдвиг по фазе между выходным и входным сигналами системы в режиме установившихся гармонических колебаний на данной частоте.
Графики функций A(w) и j(w) называются соответственно амплитудной частотной (АЧХ) и фазовой частотной (ФЧХ) характеристиками.
Указанный выше физический смысл каждой ординаты A(w) и j(w) является основанием для экспериментального получения АЧХ и ФЧХ линейных звеньев и систем.
Графики АЧХ и ФЧХ, построенные в логарифмическом масштабе, называют логарифмическими частотными характеристиками: ЛАЧХ и ЛФЧХ. Зачем нужны логарифмические частотные характеристики (ЛЧХ)? Для ответа на этот вопрос рассмотрим частотные характеристики последовательного соединения звеньев.
При последовательном соединении звеньев (см. (2.44))
W(p)=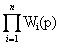 
.
Заменяя p на jw, можно записать
W(jw)= 
. (3.24)
Учитывая, что W(jw)= A(w) 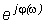(3.25)
Wi (jw)= Ai (w)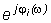 
(3.26)
и подставляя выражения (3.25) и (3.26) в формулу (3.24), получим
A(w) =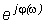 
,
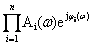откуда следует, что
A(w)=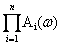 
; (3.27)
j(w) =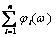 
. (3.28)
Выражения (3.27) и (3.28) показывают, что для вычисления частотных характеристик последовательного соединения звеньев необходимо для каждого из фиксированных значений частот перемножить модули ЧПФ и суммировать их аргументы. Для того, чтобы исключить операции умножения целесообразно использовать логарифмические характеристики. Из (3.27) следует:
L(w) = 20lgA(w) =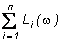 
;
Li(w) = 20lgAi(w).
Для их построения по оси абсцисс откладываются значения частот в логарифмическом масштабе. Эта ось равномерно разбивается на декады. Декада соответствует десятикратному изменению частоты (в рад/с), например, от 0,1 до 1, от 1 до 10 и т.д. Масштабирование каждой декады выполняется одинаково на основе следующего соотношения
mw = mдек × (мантисса десятичного логарифма цифр от 2 до 9),
где mдек - масштаб декады в мм,
mw - масштаб частоты от начала своей декады (своего порядка).
При построении ЛАЧХ значение модуля ЧПФ откладывается в децибелах (дБ) в равномерном масштабе. Если модуль ЧПФ A(w), то число децибел равно L(w)=20lgA(w) дБ.
При построении ЛФЧХ по оси ординат откладывается значение j(w) в градусах или радианах.
В заключение отметим, что за редким исключением строят не точные, а асимптотические ЛАЧХ (см. пример 3.1).
