Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны.
Каждый угол правильного многоугольника равен 180º (n – 2) / n, где n – число его углов.
Около любого правильного многоугольника можно описать окружность и в каждый правильный многоугольник можно вписать окружность. Центры этих окружностей совпадают и эта точка называется центром правильного многоугольника. Центр равноудален от всех вершин многоугольника и также равноудалён от всех его сторон.
Соотношения в правильных многоугольниках.
Обозначения:
п—число сторон правильного многоугольника;
аn —сторона правильного многоугольника;
R—радиус описанной окружности;
r — радиус вписанной окружности
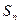 - площадь многоугольника
- площадь многоугольника
 - периметр многоугольника
- периметр многоугольника
Выражение сторон правильного многоугольника через радиус описанной и радиусвписанной окружности.


Сторона правильного n-угольника равна  , где R - радиус описанной окружности
, где R - радиус описанной окружности
Сторона правильного n-угольника равна  , где r - радиус вписанной окружности.
, где r - радиус вписанной окружности.
Правильный треугольник

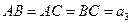




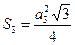
Правильный четырехугольник (квадрат)








Правильный шестиугольник







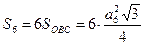
Задания с решением.
1. Сторона правильного треугольника равна  . Найдите площадь кольца, образованного окружностями, описанной и вписанной в этот треугольник.
. Найдите площадь кольца, образованного окружностями, описанной и вписанной в этот треугольник.
Решение.

Имеем для правильного треугольника формулы:  и
и  .
.
По условию 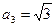 . Тогда
. Тогда  , откуда
, откуда  и
и  .
.
Площадь кольца найдем по формуле 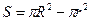

Ответ 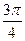
2. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
Решение

Для высоты СК верно равенство. СК=R+r
Тогда  , то есть
, то есть  , а значит
, а значит  ,
, 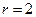
Ответ 2
3. В круг вписан квадрат. Найти площадь квадрата, если длина окружности данного круга равна 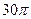
 .
.
Решение

Длина окружности находится по формуле  .
.
Получаем  .Откуда
.Откуда  .
.
По формуле для правильного четырехугольника(квадрата) имеем  , то есть
, то есть 
Тогда площадь квадрата 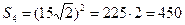
Ответ 450
4. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной  .
.
Решение


Для правильного шестиугольника выполнено  . По условию
. По условию 
Тогда 
Ответ: 3
5. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Решение
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Ответ: 6.
6. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен  . Найдите n.
. Найдите n.
Решение
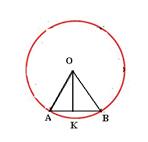
По условию угол ОАВ равен 54º.Тогда угол правильного многоугольника равен 108º. Но каждый угол правильного многоугольника равен 180º (n – 2) / n, где n – число его углов. Получаем уравнение 
Откуда 




Ответ 5
7.Разность сторон правильных треугольника и четырехугольника, вписанных в одну и туже окружность, равна 2.Найти периметр правильного шестиугольника, описанного около этой окружности.
Решение.
Для треугольника и четырехугольника окружность является описанной.

| 
|
Следовательно, верны соотношения  и
и  . Тогда получаем уравнение
. Тогда получаем уравнение  , то есть
, то есть 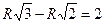


Для шестиугольника эта окружность является вписанной
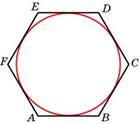
Следовательно, верно равенство  , где
, где 
Тогда  . Откуда
. Откуда 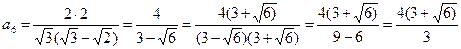
Тогда периметр шестиугольника равен 
Ответ 






