Окружность называется вписанной в четырехугольник, если все стороны четырехугольника являются касательными к окружности.
Центром этой окружности является точка пересечения биссектрис углов четырехугольника. В этом случае радиусы, проведенные в точки касания являются перпендикулярами к сторонам четырехугольника
Окружность называется описанной около четырехугольника, если она проходит через все его вершины.
Центром этой окружности является точка пересечения серединных перпендикуляров к сторонам четырехугольника
Не во всякий четырехугольник можно вписать окружность и не около всякого четырехугольника можно описать окружность
СВОЙСТВА ВПИСАННЫХ И ОПИСАННЫХ ЧЕТЫРЕХУГОЛЬНИКОВ
ТЕОРЕМА В выпуклом вписанном четырехугольнике суммы противолежащих углов равны между собой и равны 180°.
ТЕОРЕМА Обратно: если в четырехугольнике суммы противолежащих углов равны, то около четырехугольника можно описать окружность. Ее центр - точка пересечения серединных перпендикуляров к сторонам.
ТЕОРЕМА Если в четырехугольник вписана окружность, то суммы противолежащих сторон его равны.
ТЕОРЕМА Обратно: если в четырехугольнике суммы противолежащих сторон равны, то в него можно вписать окружность. Ее центр - точка пересечения биссектрис.
Следствия: из всех параллелограммов только около прямоугольника (в частности около квадрата) можно описать окружность.
Из всех параллелограммов только в ромб (в частности в квадрат) можно вписать окружность (центр - точка пересечения диагоналей, радиус - равен половине высоты).
Если около трапеции можно описать окружность, то она равнобедренная. Около любой равнобедренной трапеции можно описать окружность.
Если в трапецию вписана окружность, то радиус ее равен половине высоты.
Задания с решениями
1. Найти диагональ прямоугольника, вписанного в окружность, радиус которой равен 5.
Решение
Центром окружности, описанной около прямоугольника является точка пересечения его диагоналей. Следовательно, диагональ АС равна 2 R. То есть АС =10
Ответ: 10.
2. Около трапеции, основания которой 6 см и 8 см, а высота 7см, описан круг Найти площадь этого круга.
Решение
Пусть DC =6, AB =8. Так как около трапеции описана окружность, то она равнобедренная.
Проведем две высоты DM и CN. Так как трапеция равнобедренная, то AM=NB = 
Тогда AN =6+1=7
Из треугольника ANС по теореме Пифагора найдем АС.
Из треугольника CВN по теореме Пифагора найдем ВС.
Окружность, описанная около трапеции, является и окружностью, описанной около треугольника АСВ.
Найдем площадь этого треугольника двумя способами по формулам
, гдe h - высота и - основание треугольника
,где R- радиус описанной окружности.
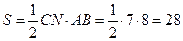
Из этих выражений получаем уравнение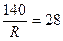 
. Откуда 
Площадь круга будет равна 
Ответ
3. Углы 
, 
и 
четырехугольника 
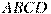относятся как 
. Найдите угол 
, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах
Решение.
Из условия следует, что 
.Так как около четырехугольника можно описать окружность, то 
Получаем уравнение 
. Тогда 
. Сумма всех углов четырехугольника равна 360º. Тогда 
. откуда получаем, что 
Ответ 90º
4.Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
Решение
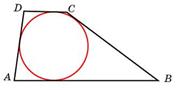
Так как в трапецию вписана окружность, то суммы длин противоположных сторон равны. Тогда 
Тогда средняя линия равна 
Ответ 4
5. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Решение
В трапеции радиус вписанной окружности равен половине высоты. Проведем высоту СК.
Тогда 
.
Так как в трапецию вписана окружность, то суммы длин противоположных сторон равны. Тогда 
Тогда периметр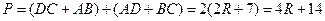 
Получаем уравнение 
Ответ 2
6. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Решение
Пусть О центр описанной около трапеции окружности. Тогда 
.
Проведем высоту КН через точку О
Тогда 
, где КО и ОН высоты и одновременно медианы равнобедренных треугольников DOC и АОВ. Тогда 
По теореме Пифагора:
= 
Тогда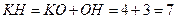 
Ответ: 7.
