- Найдите радиус окружности, вписанной в треугольник ABC, считая стороны квадратных клеток равными 1.
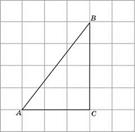
- В треугольнике ABC
, 
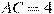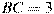, угол C равен 
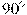. Найдите радиус вписанной окружности.
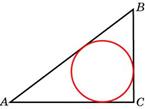
- Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
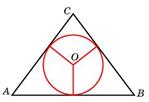
- Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 8 и 5, считая от вершины, противолежащей основанию. Найдите периметр треугольника и площадь вписанного круга.
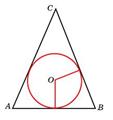
- К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
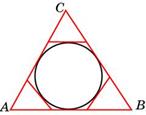
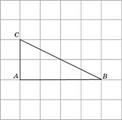
- Найдите радиус R окружности, описанной около треугольника ABC, если стороны квадратных клеток равны 1. В ответе укажите
.
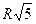- Катеты равнобедренного прямоугольного треугольника равны
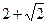. Найдите радиус окружности, вписанной в этот треугольник.
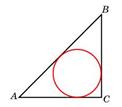
- В равнобедренном треугольнике центр вписанного круга делит высоту в отношении 17:15.основание равно 60 см. Найти площадь этого круга
- Около круга, радиус которого равен 4, описан прямоугольный треугольник, гипотенуза которого равна 26. Найти периметр этого треугольника.
- Радиус окружности, вписанной в прямоугольный треугольник, равен 4.Один из катетов равен 9.Найти второй катет.
- Радиус окружности, вписанной в прямоугольный треугольник, равен 3.Один из катетов равен 8.Найти гипотенузу.
- Окружность с радиусом 6
описана около равнобедренного треугольника с углом 120º.Найти основание треугольника. - Одна из сторон вписанного в окружность треугольника равна 24см и отстоит от центра окружности на расстоянии 5см. Найти радиус окружности.
- В треугольнике АВС внешний угол при вершине С равен 90º, а внешний угол при вершине А равен 150º.Меньшая сторона треугольника равна 12,5.Найти длину диаметра окружности, описанной коло этого треугольника.
- Расстояния от вершин треугольника до точек касания вписанной в этот треугольник окружности равны соответственно 2, 3 и 5. Найти периметр этого треугольника.
- Боковая сторона равнобедренного треугольника равна 5, а угол при основании 30º.Найти диаметр описанной окружности.
- Окружность радиусом
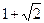описана около равнобедренного прямоугольного треугольника. Найти площадь вписанного в треугольник круга. - Сумма меньшего катета и гипотенузы равна 3.Острый угол прямоугольного треугольника равен 30º.Найти радиус описанной окружности.
- Найдите площадь круга, в который вписан прямоугольный треугольник с катетами 8 см и 6 см.
- Стороны треугольника 13 см, 14 см, 15 см. Найти радиусы вписанной и описанной окружности.
- Высота равнобедренного треугольника 4 см, основание 6 см. Найти боковые стороны и радиусы вписанного и описанного кругов.
- Найти площадь круга, описанного около треугольника со сторонами 25 см, 24 см и 7 см.
- Окружность с центром О вписана в прямоугольный треугольник АВС. Она касается гипотенузы АВ в точке М, причём АМ = 12, ВМ = 8. Найдите площадь треугольника АОВ.
- Около круга, радиус которого равен 3см, описан равнобедренный треугольник с острым углом в 30º при основании. Найти длины сторон треугольника
- Стороны треугольника равны 17, 15 и 8.Найти длину окружности, описанной около треугольника и площадь круга, вписанного в треугольник.
- В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 и 12.Найти меньший катет.
- Стороны треугольника равны 25,24 и 7.Найти длину окружности, описанной около треугольника и площадь круга, вписанного в треугольник.
Занятие 10
