Расчет Cканави Г.Л. ионно-релаксационной поляризации основан лишь на рассмотрении двух соседних сечений, отстоящих на постоянную решетку. В качестве таковых можно взять два любых сечения, перпендикулярных внешнему полю в любом месте образца. В действительности ионы могут двигаться на более протяженных участках намного превышающих параметр решетки.
Вследствие такого движения область вблизи анода будет обеднена катионами, а их концентрация вблизи катода возрастет, т.е. будет образовываться двойной электрический слой. Кроме этого будет наблюдаться обратный дрейф катионов под действием поля поляризации, а также вследствие диффузионного движения из-за возникающего градиента концентрация свободных катионов.
Следовательно, расчет Сканави Г.Л. необходимо обобщить на случай миграции ионов на макрорасстояния. В этом случае время релаксации при которой ион мигрирует на расстояние d можно описать соотношением:
, (91)
где 
, (92)
Но расстояние a можно представить как путь при дрейфе, осуществляемый за время Т/2, где Т- период колебаний иона, т.е Т=1/n0. Действительно, движение иона из потенциальной ямы и обратно осуществляется за время, равное половине периода его колебаний, поэтому допускаем лишь, что вместо своего узла ион при возврате находит соседний узел, будут «снесены» по ходу процесса полем
, (93)
, (94)
Величина d- толщина объединенного слоя. Формулу (1) можно рассматривать как общую формулу, характеризующую время релаксации миграционного процесса носителей заряда, активируемых на границах. Такие слои могут образовываться в приэлектродном слое на границах раздела фаз, имеющих различные величины электропроводности. В этом случае говорят об образовании объемного заряда.
Междуслойная поляризация
На практике часто встречается случай слоистого диэлектрика или неоднородностей, в связи с этим представляет интерес рассмотрения междуслойной поляризации. Такой случай описан Максвеллом и Вагнером.
Междуслойную поляризацию следует рассматривать как частный случай миграционной поляризации, где в общем случае могут участвовать как ионы, так и электроны. Но в отличие от рассмотренного случая миграции ионов трактовка Максвелла - Вагнера не учитывает изменения проводимости вследствие процессов миграции.
Рассмотрим двухслойный диэлектрик (рис.) Положим, что все диэлектрические параметры остаются неизменными, несмотря на миграцию зарядов. Предположим, что диэлектрические проницаемости и электропроводности слоев постоянны (
, 
, 
, 
.- const), а 
, 
- толщина слоев. Допустим, что 
; 
(рис.)
В первый момент включения напряжения V0 приложенного к обкладкам конденсатора напряженность поля распределяется в соответствии с величиной диэлектрической проницаемости при этом вектор электрической индукции D должен быть непрерывным и равным:
, (95)
Изменение потенциала будет согласно кривой 1(рис.), где 
и 
- напряженность поля в слоях 1 и 2 в начальный момент времени:
, (96)
, (97)
, (98)
Подставляя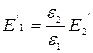 
и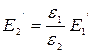 
в (98) получим соотношения:
, (99)
(100)
Предположим, что процесс равновесия уже установлен и образец находится под напряжением V0. В этом случае необходимо учесть условие равновесия токов проводимости.
, (101)
- плотность тока, 
и 
- напряженности поля при установленном равновесии которые равны:
, (102)
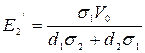, (103)
Если бы 
и 
, то получили бы E1'=E1” и Е2’=E2”
Следовательно, в таком двухслойном диэлектрике релаксация Максвелла-Вагнера отсутствует.
Если Е1' 
E1” и Е2’ E2” в таком диэлектрике наблюдается релаксация Максвелла-Вагнера. Определим теперь указанную релаксацию.
Запишем условие непрерывности плотности полного тока, состоящего их тока проводимости и тока смещения.
, (104)
Для текущих значений напряженности поля
, (105)
следовательно:
, (106)
, (107)
, (108)
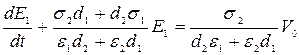, (109)
Решение будем искать в виде:
, (110)
- 
, 
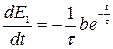, (111)
, (112)
, (113)
, (114)
В начальный момент времени при t=0, 
, (115)
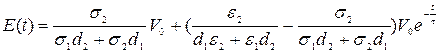, (116)
, (117)
При 
, (118)
При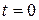 
, (119)
Полученные соотношения (117), (118), (119) позволяют записать в явном виде выражения для плотности тока:
, (120)
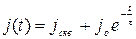, (121)
Удельные электропроводности и обычно определяют по остаточному току, которые обусловлены сквозной электронной проводимостью. Спад тока происходит по закону экспоненты, причем он обусловлен накоплением заряда на границе раздела слоев. Этот заряд создает встречную Э.Д.С. поляризации, которая и вызывает этот спад (рис).
При подаче потенциала на границе раздела накапливается заряд. После снятия внешнего напряжения наблюдается встречное поле в первом и втором слое. При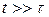 
заряд релаксирует, поле исчезает и потенциал обращается в нуль.
Таким образом, Максвелл-Вагнеровская поляризация состоит в накоплении заряда на границе раздела слоев вследствие протекания токов проводимости в двухслойном образце, вызывающем перераспределение электрических полей и падений напряжения в слоях. Процесс заканчивается при t>>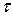 
, когда остается лишь сквозная составляющая проводимости. При выключении внешнего напряжения наблюдается деполяризация.
      |
И-Э- инжекторно-электронная
С-П- скачковая проводимость
М- миграционная
М-С- междуслойная
С- структурная
Диапазон частот, характерный для данного вида поляризации.
| Виды поляри-зации | Э-Д | Э-Д | Э-Д И-Д | Э-Д И-Д | 1. Э-Д 2. И-Д 3. Э-Р 4. И-Р 5. Д-Р 6. И-Э 7. С-П | 8. М 9. МС 10. С | ||
| Частот-ный диапа-зон | УФ | Опти-чес-кий | И-К | СВЧ | Радиочастотный |
10-16 10-14 10-12 10-10 10-8 10-6 10-4 10-2 1 101 102 t(с)
1013 109 105 
(гц)
