ОСНОВНЫЕ МОДЕЛИ ПОЛЯРИЗАЦИИ ДИЭЛЕКТРИКОВ
Исходя из структуры диэлектрика, в нем может реализоваться различные механизмы поляризации. В данном разделе приводятся основные, наиболее часто встречающиеся случаи поляризации диэлектриков.
Эффективное поле в диэлектрике
Диэлектриками с идеальной структурой являются твердые тела без свободных носителей заряда. В таких диэлектриках все заряженные частицы взаимосвязаны, они не могут приобретать ускорения под действием внешнего поля.
Электрическое поле характеризуется двумя векторами напряженностью 
и индукцией 
электрического поля, что следует из уравнений Максвелла:
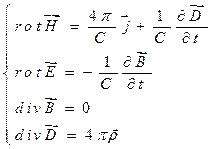(1)
Фарадей установил, что при введении диэлектрика между обкладками конденсатора происходит увеличение его емкости С. Электрический заряд q обкладки конденсатора остается неизменным, а разность потенциалов Δφ уменьшается.
, (2)
Этот эффект возможен в результате поляризации диэлектрика. Часть 
заряда обкладки конденсатора оказывается связанной с противоположным зарядом, образующимся на поверхности диэлектрика. При этом часть заряда q2 остается свободной. Полный заряд определяется как сумма связанного и свободного заряда:
q = q1 + q2, (3)
Возможность диэлектрика поляризоваться является следствием электрической структуры диэлектрика, электроны и ионы могут смещаться под действием поля. Состояние макроскопического поля в диэлектрике описывается вектором индукции и вектором напряженности электрического поля . Между и существует взаимосвязь.
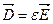, (4)
где 
- диэлектрическая проницаемость среды.
Напряженность электрического поля можно сопоставить со свободным зарядом 
. Индукцию - с полным зарядом q. Связанный заряд q1 описываться величиной, отражающей смысл поляризации диэлектрика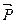 
, который обусловлен наличием связанных зарядов, т.е. наличием диполей:
, (5)
где е – заряд и l – расстояние между зарядами в диполе.
Напряженность электрического поля диполя на расстоянии r выражается в виде
, (6).
Вектор поляризации 
равен электрическому моменту, отнесенному к единице объема диэлектрика. Нетрудно видеть, что в соответствии с (3) векторы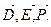 
должны быть связаны равенством:
, (7)
Из выражения (4) и (7) следует:
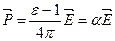, (8)
где 
- коэфицент поляризуемости диэлектрика.
В теории Максвелла предполагается, что диэлектрическая проницаемость является постоянной характеристикой диэлектрика. Опыты показывают, что она зависит от длины волны. Электродинамика полностью не раскрывает природы диэлектрической постоянной. Поэтому задачей данного курса является выяснение микроструктуры диэлектрической проницаемости. Важную роль при определении микроструктуры играет понятие эффективного поля в диэлектрике.
При рассмотрении микроструктуры диэлектрической постоянной необходимо вычислить эффективную напряженность Eэф, действующую на атом или молекулу. Для вычисления эффективной напряженности будем использовать метод Лоренца.
Выберем часть диэлектрика и разобьем его на две области (рис). Поместим молекулу в точку М и построим вокруг нее сферу, радиус R которой значительно превышает линейный размер а молекулы (R>> a), но мал по сравнению с макроскопическими неоднородностями диэлектрика. Эффективное поле Еэф, действующее на молекулу расположенную внутри диэлектрика, будет равно сумме полей создаваемых молекулами диэлектрика внутри и вне сферы:
, (9)
где 
- напряженность, создаваемая в точке М молекулами диэлектрика внутри сферы (область А);
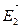- напряженность, создаваемая в точке М молекулами диэлектрика вне сферы (область В).
Так как радиус сферы намного больше размера молекулы (R>> a), то при вычислении 
можно рассматривать область «В» как сплошную среду. При этом:
, (10)
где - средняя напряженность макроскопически однородного поля; 
- напряженность однородного поляризованного шара (область А).
, (!!)
При вычислении напряженности поля E1 внутри сферы (область А) ее нельзя рассматривать как сплошную среду, так как влияние близких к точке М молекул существенно зависит от их взаимного расположения и взаимодействия. Поэтому E1 можно найти только при определенных предположениях о строении диэлектрика. Если дипольные моменты 
молекул, находящиеся внутри сферы (область А), расположены беспорядочно, то среднее значение равно нулю.
Действительно для изотропной среды внутри сферы (область А) в соответствии с соотношением (6) усредненное значение напряженности электрического поля, создаваемое несколькими молекулами, обладающими дипольным моментом на выбранное направление х определяется соотношением:
, (12)
и при условии, что 
; 
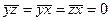равно нулю.
Полученные соотношения (9), (10), (11), (12) позволяют вычислить эффективную напряженность поля внутри диэлектрика:
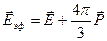, (13)
где 
- молекулярное поле Лоренца.
