В полярных диэлектриках молекулы имеют готовый электрический момент. Если внешнего поля нет, то результирующий момент равен нулю (рис). Приложение электрического поля к диэлектрику приводит к ориентации диполей по полю и возникает поляризация диэлектрика. Энергию диполей находящихся в электрическом поле можно описать соотношением:
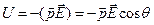, (46)
где θ – угол между вектором поляризации диполя и напряженностью электрического поля Е. Наименьшую энергию имеют диполи, ориентированные по направлению поля (θ = 0), а наибольшую - против поля θ = π). Максимальная поляризуемость может быть достигнута при низких температурах Т≈ 0.
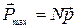, (47)
С повышением температуры возрастает разупорядоченность диполей и уменьшается поляризация диэлектрика.
Предположим, что вероятность dW найти молекулу с дипольным моментом р и потенциальной энергией U ориентированным в элементе телесного угла dΩ равна:
, (48)
где элемент телесного угла:
, (49)
а вероятность состояния молекулы с потенциальной энергией U при данной температуре определяется выражением:
, (50)
Поляризацию диэлектрика в одном из выбранных направлений Pz можно найти, как сумму проекций всех дипольных моментов pi,z молекул, расположенных в единице объема диэлектрика на направление Z:
(51)
Общая поляризация диэлектрика в направлении действия поля Еz:
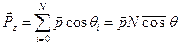, (52)
Значение среднего косинуса может быть вычислено по формуле:
, (53) в этих вычислениях сделана замена переменной 
; 
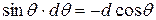и определены приделы интегрирования для угла θ от 0 до π (для η от -1 до +1) и для угла φ от 0 до 2 π. При вычислениях сделана замена
а = рЕ/кТ, (54)
Не трудно видеть, что интеграл в числителе (53) представляет собой первую производную интеграла знаменателя:
, (55)
, (56)
Согласно полученным соотношениям (53), (55) и (56) усредненный косинус будет равен:
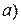, (57)
где L(a) функция Ланжевена.
Подставляя полученное выражение (57) в (52) получим соотношение, которое определяет зависимость поляризации диэлектрика от напряженности электрического поля и температуры:
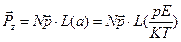(58)
Функцию Ланжевена можно представить графически (рис).
Если диэлектрик находится при высоких температурах и небольших величинах напряженности электрического поля то 
при этом
L(a) =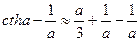 
, (59)
В области малых полей 
и
, (60)
Сопоставляя соотношение (60) с (8) получим выражение для диэлектрической проницаемости:
, (61)
При низкой температуре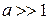 
и Функция Ланжевена 
Разделив обе части уравнения (43) на количество дипольных моментов в единице объема 
получим среднее значение проекции электрического момента молекулы на направление электрического поля 
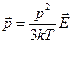, (62)
, (63)
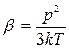, (64)
Если в структуре диэлектрика есть молекулы, обладающие индуцированными и готовыми дипольными моментами, то формула для молярной рефракции будет состоять из двух слагаемых:
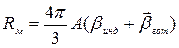, (65)
, (66)
Согласно этой формуле из экспериментальной зависимости молярной рефракции от обратной температуры можно определить дипольный момент молекулы:
. (67)
