В неполярных диэлектриках в отсутствии внешнего электрического поля молекулы или атомы не имеют электрического момента. Под воздействием внешнего электрического поля возможно смещение электронных оболочек атомов относительно ядер и возникновение индуцированного электрического момента (рис) Для таких диэлектриков выполняется равенство:
, (14)
где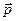 
- электрический момент диполя, β – коэффициент поляризуемости молекулы.
Поляризация диэлектрика 
, равная по величине электрическому моменту единицы объема и связана с электрическим моментом 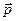молекулы равенством:
, (15)
где N –число молекул в единице объема диэлектрика.
Полученные соотношения (13), (14) и (15) позволяют установить связь между поляризацией диэлектрика Р и напряженностью электрического поля Е: 
, (16)
Сравнивая полученное соотношение (16) с (8) можно получить выражение для диэлектрической проницаемости:
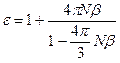, (17)
Это выражение характеризует микроструктуру диэлектрической проницаемости в неполярных диэлектриках. Диэлектрическая проницаемость в таких диэлектриках определяется концентрацией молекул N и их поляризуемостью β. Полученное соотношение (17) содержит величины, которые трудно определить экспериментально. Поэтому на практике пользуются формулами Клаузиуса- Моссоти и Лоренц-Лорентца
При расчете на 1моль вещества концентрацию молекул можно представить в виде:
, (18)
где А- число Авогадро, М- масса грамм/моля.
Преобразуем полученное выражение (17) в более удобный вид. Для этого прибавим к правой и левой части выражения по три единице и поделим полученные соотношения между собой:
, (19)
Подставим выражение (18) в (19) и получим формулу, известную в литературе, как формула Клаузиуса- Моссоти:
, (20)
Как известно из теории Максвелла 
, где μ – магнитная проницаемость веществ. В слабомагнитных веществах, какими являются диэлектрики μ = 1 и 
. Учитывая эти соотношения, можно получить формулу Лоренц – Лоренца.
, (21)
Полученные формулы Клаузиуса – Массоти и Лоренц – Лоренца позволяют экспериментально проверить теорию, в основе которой лежат представления об индуцированных электрических зарядах. На практике при исследовании диэлектрических характеристик веществ пользуются величиной молярной рефракции RM, которая определяется выражениями:
, (22)
, (23)
Так как показатель преломления n является безразмерной величиной, а отношение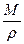 
равно объему грамм-молекулы, то RM имеет размерность объема.
Экспериментально показано, что молярная рефракция не зависит от изменения плотности вещества, внешнего давления и агрегатного состояния вещества. Это можно объяснить тем, что внешнее воздействие не приводит к изменению структуры молекулы, а следовательно и коэффициента поляризуемости β.
Обнаруживаемая устойчивость молярной рефракции подтверждает справедливость формулы Лоренц – Лоренца и отражает связь между микро- и макрохарактеристиками диэлектрика с индуцированными электрическими моментами. Полученные результаты можно обобщить для диэлектрика, состоящего из молекул разных сортов.
Пусть Nk – число молекул k-го сорта в единице объема. Тогда вместо выражения:
, (24)
где pk-электрический момент молекулы k-го сорта; S- число сортов. Пусть βk - поляризуемость молекул k-го сорта, тогда:
, (25)
Сравнивая (25) с (13) и (14) можно заключить, что
, (26)
Сделаем замену коэффициента поляризуемости β в формуле для молярной рефракции (22) и получим
, (27)
где отношение 
равно концентрации 
молекул k-го сорта. Величина Rkявляется молярной рефракцией молекул k-го сорта:
, (28)
Из полученных соотношений следует, что молярная рефракция обладает свойством аддитивности:
, (29)
Таким образом, молярная рефракция смеси молекул различных сортов аддитивно складывается из молярных рефракций компонент, умноженных на соответствующие им концентрации.
